𝐏𝐚𝐫𝐭 𝟑: 𝐐𝐮𝐚𝐧𝐭𝐢𝐭𝐚𝐭𝐢𝐯𝐞 𝐑𝐞𝐚𝐬𝐨𝐧𝐢𝐧𝐠 (Atleast, 160 পেতে হেল্প করবে এমন সাজেশন)

Exam Format

সময়ঃ ৪৭ মিনিট (২১+২৬, দুইটা সেকশন মিলে)

প্রশ্নঃ ২৭ টি প্রশ্ন(১২+১৫, দুইটা সেকশন মিলে)।

মার্কঃ 130–170, in 1-point increments [মূলত ৪০ নম্বর]

Scoring(difficulty level): মনে রাখবে, quant এ- ১ম সেকশনে ভাল করতে হবে, তাহলে ওভারঅল ভাল স্কোর সম্ভব।
quant এ-১ম সেকশনে 12 questions এর difficulty লেভেল(আনুমানিক)-

• difficulty level:1:- 1/2 টা
• difficulty level 2:- 1/2 টা
• difficulty level 3:- 6/7 টা
• difficulty level 4:- 1 টা
• difficulty level 5:- 1 টা

quant এ-২য় সেকশনে 15 questions এর difficulty লেভেল(আনুমানিক)-

• difficulty level 1:- 1/2 টা
• difficulty level 2:- 1/2 টা
• difficulty level 3:- 3/4 টা
• difficulty level 4:- 3/4 টা
• difficulty level 5:- 5/6 টা

Types of Questions: Quantitative Comparison, Multiple Choice (One Ans), Multiple Choice(One or More), Numeric Entry.

Quantitative Comparison: দুইটা Quantity দেওয়া থাকবে- Quantity A ও Quantity B । এক্ষত্রে, কখনো একটি বড় হতে পারে/ছোট হতে পারে / দুইটাই সমান হতে পারে / undefined একেকবার একেকরকম result – এই চার রকমের answer হতে পারে।

Numeric Entry: এক্ষেত্রে answerটা type করে বসাতে হয়। এক্ষেত্রে আবার অনেক সময় স্পেসিপিক বলে দেওয়া হয় যেমন- দশমিকের পর ২ ডিজিট রাখবেন, nearest whole নাম্বারে রাখবেন(যেমন- এক্ষেত্রে 16.5 থাকলে 17 লিখতে হবে) ইত্যাদি। [এগুলা ২টার মত আসে]

Multiple Choice (One Ans): যেকয়টা/পাঁচটা অপশন থাকে, যার মধ্য থেকে শুধুমাত্র একটাই correct answer হবে। এক্ষত্রে, শুধুমাত্র বৃত্তাকার shape এর answer option দেয়া থাকে।

Multiple Choice(One or More): যেকয়টা অপশন থাকে, তার মধ্য থেকে কয়েকটা কিংবা একটা correct answer হবে। এক্ষত্রে, দুইটা জিনিস দেখে এ টাইপটা বুঝা যা- (১) indicate all such values (২) square shape এর answer option দেয়া থাকে। [পরীক্ষায় এগুলা ২-৩টার বেশি আসবে না]

Number of Questions(Approximate): পরীক্ষা বিভিন্ন প্রশ্ন প্যাটার হয়ে থাকে। যেমন-

• Section 1: Quantitative Comparison 4টা + Numeric Entry 1/2টা + Multiple Choice(One or More) 1/2টা
• Section-2: Quantitative Comparison 5টা + Numeric Entry 1/2টা + Multiple Choice(One or More) 1/2টা

যে টপিক হতে যেকয়টি প্রশ্ন করা হয়ঃ বিভিন্ন Types of Questions থাকায়, (approximately) ১ম সেকশনে ৪টা math আর ২য় সেকশনে ৫টা math এরকম থাকতে পারে(এর ব্যতিক্রম হতে পারে)। + ১ম সেকশনের সেটে must ৩টা Data interpretation ম্যাথ questions আসে, ২য় ধাপে আবার এটা আসতে দেখা যায় না। +

Quant Math সিলেবাসঃ

1. Arithmetic (পাটিগনিত)
1.1 Integers(/Number System)
1.2 Fractions
1.3 Exponents and Roots
1.4 Decimals
1.5 Real Numbers
1.6 Ratio
1.7 Percent

আমাদের সুবিধার্থে Arithmetic এর এই সিলেবাস এর বিস্তারিত ভার্সনকে দুইটা পার্টে ভাগ করে পড়ব- 

Topics Part 1: Basic Math Terms & Symbols || Integer(/Number System): Positive, Negative || Basic operations: Odd, Even,Mutiply,Division || Consecutive numbers|| Divisibility {Unit Digit + Remainder} || Factors, Multiples || Prime Numbers, || HCF and LCM

Topics Part 2: Fractions, Decimals || Exponents, Square, Cube, Square root, Cube root || Real Number, Number Line, Inequalities and Absolute Value, Reciprocals || Ratios  || Proportion || Percent

2. Algebra (বীজগণিত)
2.1 Algebraic Expressions
2.2 Rules of Exponents
2.3 Solving Linear Equations
2.4 Solving Quadratic Equations
2.5 Solving Linear Inequalities
2.6 Functions
2.7 Applications
2.8 Coordinate Geometry
2.9 Graphs of Functions

3. Geometry (জ্যামিতি)
3.1 Lines and Angles
3.2 Polygons
3.3 Triangles
3.4 Quadrilaterals
3.5 Circles
3.6 Three-Dimensional Figures

4. Data Analysis (ডেটা এনালাইসিস)
4.1 Methods for Presenting Data
4.2 Numerical Methods for Describing Data
4.3 Counting Methods
4.4 Probability
4.5 Distributions of Data, Random Variables, and Probability Distributions
4.6 Data Interpretation Example

(For Exam Day Preparation: selected topics) যেসব টপিক হতে প্রশ্ন আসার সম্ভাবনা বেশি-

 

বই (প্রস্তুতি)

Preparation: সিরিয়ালি দুইটা স্টেপ অনুসরণ করে/পদ্ধতিতে প্রিপারেশন নেব:-

1. • [Concept জানার জন্য] :» Basic Knowledge » • Important Formulas » • Shortcut Techniques
2. • [Practice এর জন্য] :» Practice Problems » • Test Taking Strategies » • Personal Hand Note(Mistakes & improvement)

1. [Concept এর জন্য] আপনি যদি আগে ম্যাথ পড়া না থাকে, তাহলে –
১) 𝐌𝐚𝐧𝐡𝐚𝐭𝐭𝐚𝐧 𝟏-𝟔 𝐬𝐞𝐫𝐢𝐬 [(𝐌𝐚𝐧𝐡𝐚𝐭𝐭𝐚𝐧 এর GRE All the Quant বা 𝐌𝐚𝐧𝐡𝐚𝐭𝐭𝐚𝐧 এর Math Strategies) – এই ৩টা বই-ই একই ধরনের, তাই যেকোনো একটা ফলো করলেই  হবে]

২) 𝐌𝐚𝐧𝐡𝐚𝐭𝐭𝐚𝐧 𝟓𝐥𝐛 (বিগেনার লেবেলে হেল্প করে) [এটার ২টা edition আছে, যেকোনো একটা পড়লেই হবে] তবে- Manhattan 5lb (3rd edition) : Chapter 7-30 [এটা সুবিধা হচ্ছে topic wise দেয়া আছে, আর পরামর্শ থাকবে এ বইয়ের পেছনে থাকা solution গুলো ফলো না করা কারণ ঐগুলা হুদাই পেঁচিয়ে জটিল করে দেওয়া হয়েছে, তাই অনলাইন থেকে সল্যুশন বের করাটাই বেস্ট]
(ক্যাটাগরি)
1. Arithmetic – 7, 11, 12, 13, 15, 20 (Total 6chapters)
2. Algebra – 8,9,10,14,16, 17,18,19 (Total chapters)
3. Geometry – 25, 26, 27, 28, 29 (Total Schapters)
4. Data Interpretation – 21, 22, 23, 24 (Total 4chapters)
» বেসিক জিনিসগুলোর ধারণা একদম ক্লিয়ার শেখার জন্য– Saifurs English, Khairul’s Basic Math (পাটিগণিত, বীজগণিত এবং জ্যামিতি চ্যাপ্টার) বা NCTB Class Five to Nine Math Books (If Possible)
» শর্টকাট শেখার জন্যঃ Note করতে হবে + যেকোনো একটি বই ফলো করতে হবে।

অথবা, আর যদি ম্যাথ মোটামুটি করা থাকে, তাহলে –
১) 𝐁𝐨𝐛 𝐌𝐢𝐥𝐥𝐚𝐫 𝐆𝐑𝐄 𝐌𝐚𝐭𝐡
২) 𝐌𝐜𝐆𝐫𝐚𝐰 𝟓𝟎𝟎 𝐐𝐮𝐚𝐧𝐭 𝐏𝐫𝐚𝐜𝐭𝐢𝐜𝐞
» Magoosh (Optional)- Magoosh GRE Quant Practice Questions (More than 600 questions) & Magoosh GRE Math Tutorials Videos (About 200 Videos) এগুলোর সাথে এখনকার ets test এর standard মিল নাই, তাছাড়া হুদাই কঠিন টাইপের ও সেকেলে হয়ে গেসে। তাই ফলো করা না করা আপনার ইচ্ছা।

2. [Practice এর জন্য] এরপর একটানা প্রাক্টিস করার জন্য –
৩) (ETS) 𝐆𝐑𝐄 𝐌𝐚𝐭𝐡 𝐑𝐞𝐯𝐢𝐞𝐰 [টপিকওয়াইজ প্রাক্টিস করার জন্য] (এটাই মূলত সিলেবাস, যা অনেকেই জানেনা)
৪) (ETS) 𝐆𝐑𝐄 𝐐𝐮𝐚𝐧𝐭𝐢𝐭𝐚𝐭𝐢𝐯𝐞 𝐑𝐞𝐚𝐬𝐨𝐧𝐢𝐧𝐠
৫) (ETS) 𝐆𝐑𝐄 𝐎𝐟𝐟𝐢𝐜𝐢𝐚𝐥 𝐆𝐮𝐢𝐝𝐞
৬) 𝐃𝐢𝐟𝐟𝐢𝐜𝐮𝐥𝐭𝐲-𝐰𝐢𝐬𝐞 𝟓𝟎𝟎 𝐪𝐮𝐞𝐬𝐭𝐢𝐨𝐧𝐬
৭) 𝐓𝐨𝐩𝐢𝐜-𝐰𝐢𝐬𝐞 𝟔𝟎𝟎 𝐪𝐮𝐞𝐬𝐭𝐢𝐨𝐧𝐬
৮) KMF 1147math

ফাইনালি, Mock Test

চাইলে-

• ETS GRE BIG BOOK এর 16-20 Quant Section টা ফলো করতে পারেন (Data Interpretation এর জন্য এটা ভালই)
• Nova GRE Math Bible (Geometry and Counting এর জন্য মোটামুটি ভাল)
• GMAT Quant Review এর 180-200 এর মত প্রশ্ন যেগুলো দেয়া আছে ঐগুলা প্র্যাকটিস করতে পারেন। আর, GMAT Official Guide থেকে algebra এর words problems(distance,velocity,mixture,profit,age,etc) গুলা প্রাকটিস করা ভালই
• Attempt ETS GRE Power Prep
• ETS Power Prep Plus Question 240Qs+

Tips, Tricks & Teqniques (All)

answer করার টেকনিকগুলো/কৌশলঃ

1. * Quant এর ১ম সেকশনে চেষ্টা করবেন যতটা সম্ভব বেশি উত্তর করতে। চেষ্টা করবেন কমপক্ষে যেন ১৭/১৮ টা কারেক্ট হয়।
2. * সমস্যাটি ভালোভাবে বুঝে নিন এবং কী কী টেকনিক বা সুত্র প্রয়োগ করা যেতে পারে তা ভাবুন। তারপর শুরু করুন।
3. * মেন্টাল ক্যালকুলেশনের প্রতি জোর দিন এবং ক্যালকুলেটর ও রাফ পেপার যতটা সম্ভব কম ব্যবহার করুন।
4. * কোনো প্রশ্নে অতিরিক্ত বেশী সময় (২ মিনিটের বেশী) ব্যয় করবেন না। প্রয়োজন হয় ২/৩ বার রিপিট করবেন।
5. * Quant এ সকল ইনফরমেশনই দেয়া থাকে, তাই মনোযোগ, দিয়ে প্রশ্ন বা চিত্র পড়ুন, প্রয়োজনীয় তথ্য খুঁজুন।
6. * Quant comparison এ exact মান বের করা লাগে না, শুধু বড়/ছোট বের করতে পারলেই হয়, তাই অতিরিক্ত ক্যালকুলেশনের কোনো দরকার নেই।
7. * আমার একটি পছন্দের টেকনিক আছে “মনে করি”। এসব ক্ষেত্রে নির্দিষ্ট মান দেয়া থাকেনা, সেসব ক্ষেত্রে এই টেকনিকটি সর্বাপেক্ষা উপকারী। তবে মান ধরার সময় পজেটিভ, নেগেটিভ, ০, ১ এবং দশমিকের কথা ভুলবেন না।
8. * অধিকাংশ সমস্যার ক্ষেত্রে “process of elimination” অনেক উপকারী। প্রশ্নে দেয়া শর্ত অনুসারে যেসব অপশন গুলো হতে পারে সেগুলো রেখে বাকি অপশনগুলো সব বাদ দিয়ে দিন/কেটে দিন।
9. * ets এর quant এর নিয়মগুলো ভালোভাবে জেনে ও বুঝে নিবেন এবং পরীক্ষার সময় সেগুলো ভুলে যাবেন না। যেমন, জ্যামিতিতে চিত্রগুলো স্কেল অনুসারে থাকেনা, তবে স্থানাঙ্ক জ্যামিতিতে স্কেল অনুসারে থাকে, আবার রুট থাকলে শুধু পজিটিভ মানটাই হবে, নেগেটিভটা নয় ইত্যাদি।
10. * যেহেতু নেগেটিভ মার্কিং নেই তাই কোনো প্রশ্নই খালি রেখে আসবেন না। আর যেহেতু কোনো প্রশ্নই খালি রেখে আসবেন না তাই সময়ের দিকে বার বার খেয়াল রাখুন এবং বাসায় মডেল টেস্ট দেয়ার এবং শলভ করার সময় দেখবেন সময়ের মধ্যেই সব শেষ হয়েছে কিনা।

পরামর্শঃ

• পরীক্ষায় দেখা যায় যে, মাল্টিপল চয়েসের উত্তর গুলার মধ্যে দুই তিনটাই দেখতে সঠিক/একই মনে হয়, পাঁচটি answer অপশনের মধ্যে তিনটার মধ্যেই ওরা ট্র্যাপ সেট করে রেখেছে, এ থেকে নিজেকে উত্তীর্ণ করতে হবে। এক্ষেত্রে বেস্ট হয়, প্র্যাকটিস করে নিজেকে যাচাই করার মাধ্যমে আপনি নিজে কোনটায় কোনটায় ভুল করতেছেন ওগুলা ট্র্যাক(note) করে রাখা।
• জিআরই’র গণিতের কিংবা কোয়ান্ট সেক্শনের জন্য আগে বই থেকে থিওরি কিংবা বেসিক Concept/আইডিয়া নিয়ে নিতে হবে. তারপর করতে হবে সমস্যা সমাধানের কাজ যা প্র্যাকটিস এর মাধ্যমে চালিয়ে যেতে হবে.
• তারপর আসে কি করে দ্রুত এবং অল্প সময়ের মধ্যে গণিতের সমস্যাগুলো সমাধান করা যায়। জিআরই’র জন্য একটি শর্টকাট ম্যাথ বই যেমন- Rapid Quantitative Aptitude – With Shortcuts & Tricks for Competitive Exams by Disha Experts. শর্টকাট দরকার আছে সত্য কিন্তু তার থেকে বেশি সত্য আমাদের নিজেদের গণিতের ক্যালকুলেশন স্পিড বাড়ানো.

Topic: Basic Math Terms & Symbols – বিভিন্ন ম্যাথ টার্ম ও চিহ্ন

• digit = = অঙ্ক / সংখ্যা(প্রতীক)[আলাদাভাবে]
• number = সংখ্যা[একত্র]
• prime number = মৌলিক সংখ্যা
• Integer = পূর্ণ সংখ্যা
• mix number = মিশ্র সংখ্যা
• Decimal = দশমিক (সংখ্যা)
• Consecutive number = ধারাবাহিক সংখ্যা
• Ratio – অনুপাত
• Velocity – বেগ
• Factor – উৎপাদক

• fraction = ভগ্নাংশ(প্রকৃত)
• Improper fraction = অপ্রকৃত ভগ্নাংশ
• numerator = লব
• denominator = হর

• Even = জোড়
• Odd = বিজোড়

• adding = যোগ [যোগফল(sum)]
• substracting/ deducting = বিয়োগ [বিয়োগফল(Difference)]
• multipling/multiply = গুণ [গুণফল(product)]
• devisor (ভাজক)
• dividend (ভাজ্য)
• deviding = ভাগ [ভাগফল(Quotient)]
• remainder = ভাগশেষ

যোগফল(sum/total)# অংকের মধ্যে যেসব Word গুলো থাকলে আমরা যোগ করবো?:-

• sum(of),
• add, plus, combined, total, all,
• and
• more than, increase, etc

বিয়োগফল(Difference)# অংকের মধ্যে যেসব Word গুলো থাকলে আমরা বিয়োগ করবো:-

• substracting,
• deducting

গুণফল(product)# অংকের মধ্যে যেসব Words গুলো থাকলে আমরা গুণ করবো?:-

• multiplied by
• of, product of
• twice, thrice
• double, triple
• half, one third, two thirds
• times, times as much, etc

ভাগফল(Quotient)# অংকের মধ্যে যেসব Words গুলো থাকলে আমরা ভাগ করবো?:-

• deviding

# অংকের মধ্যে যেসব Word গুলো থাকলে আমরা সমান চিহ্ন দেবো?:-

• equals, is, is the same as
• has, was, will, be
• costs
• adds up to
• results, etc

চিহ্ন – Symbol & Meaning list:-

• ‘”='” (equals sign [সমান])
• “≠”  (is not equal to sign[অসমান])
• “~” (is similar to (অনুরূপ) // used for mathematical relations)
• “≈” ( “is congruent to(সর্বসম) / approximately equal / ALMOST EQUAL TO”, is for numerical data, homeomorphism) like 𝜋≈3.14
• “≃” (ASYMPTOTICALLY EQUAL TO/ is for homotopy equivalence)
• “⩰”  (APPROXIMATELY EQUAL TO)
• “≅” (is for isomorphism, congruence, etc,  // often used in modular arithmetic to state a congruence relation)
• “≐” (used for “is defined as”)
• “≡” (used for equivalence)
• ± (Plus or minus[যোগ বা বিয়োগ])
• “||” (parallel to[সমান্তরাল])
• ⊥ (is perpendicular[লম্ব])
• |x| (Absolute value of x)

#

• L.H.S. left hand side of an equation or inequality (বামপক্ষ)
• R.H.S. right hand side of an equation or inequality (ডানপক্ষ)
• “<” {L.H.S. is less than R.H.S (ছোট)}
• “>” {L.H.S. is greater than R.H.S (বড়)}
• ≤ (L.H.S. is less than or equal R.H.S[ছোট বা সমান])
• ≥ (L.H.S. is greater than or equal R.H.S বড় বা সমান])

Exponent: Exponent 2³ means 2x2x2 = 8

আমরা জানি শুধুমাত্র ঋণাত্মক যেকোনো (জোড়/বিজোড়)সংখ্যার,  বিজোড় সংখ্যক Exponent করলে  = ঋণাত্মক হয়। বাকিসব ক্ষেত্রে ধনাত্মক হয়।

(2)² = 4 (2×2)

(-2)² = 4 (-2 x -2)

(2)³ = 8 (2x2x2)

(-2)³ = -8 (-2 x -2 x -2)

(-3)² = 9 (-3 x -3)

(-3)³ = -27 (-3 x -3 x -3)

Root:  2 = √4 বা, 2² = 4 (এটা অনেকটা exponent এর উল্টো)

Factorial: কোন সংখ্যার ফ্যাক্টোরিয়াল বলতে বুঝায় ১ থেকে শুরু করে ঐ সংখ্যা পর্যন্ত প্রত্যেকটি স্বাভাবিক সংখ্যার ক্রমিক গুণফল।
যেমনঃ 5! = 1 x 2 x 3 x 4 x 5 = 120
ফ্যাক্টোরিয়াল প্রযোজ্য কেবল মাত্র স্বাভাবিক সংখ্যার {N} জন্য। একে আশ্চর্যবোধক চিহ্ন (!) দ্বারা প্রকাশ করা হয়।

Imaginary nummber: i² = −1 বা √-1 = i. যেমন- 3i, 7i, -2i, √i

• i = √-1
• i² = -1
• i³ = -i
• i⁴ = +1
• i⁴ⁿ = 1
• i^4n-1= -i etc

Topic: Basic operations (Even, Odd, Multiply, Division)

Order of Operations: (PEMDAS বা BODMAS)

• Parenthesis (brackets)
• Exponents
• Multiplication
• Division
• Addition
• Subtraction

৩ ও ৪ নং এ PEMDAS rule এ দুটো দুটো করে একসাথে লিখার কারণ-

• আগে ‘ভাগ’, পরে ‘গুণ’ এমন কোনো নিয়ম আসলে নাই। যোগ আগে, বিয়োগ পরে এমন কোনো কথা নাই।
• ১. যে অপারেশনের অগ্রাধিকার বেশি, তাকে আগে হিসেব করতে হবে।
• ২. যদি একই অগ্রাধিকারের অনেকগুলো অপারেশন থাকে তাহলে ‘বাম থেকে ডানে’ হিসেব করতে হবে

 

#
13-5+3-2+2
= 13+3+2-5-2
= 18-7
= 11

Even numbers(জোড় সংখ্যা): end with 0, 2, 4, 6, 8 (those numbers that are completely divisible by 2)

0 is even because 0 = (2 × 0) + 0

* General formula for Even Number: 2n (n is integer)

Odd Numbers(বিজোড় সংখ্যা): end with 1, 3, 5, 7, 9

1 is odd because 1 = (2 × 0) + 1

* General formula for Odd Number: 2n-1 (n is integer)

# Even এবং Odd সংখ্যার, যোগের নিয়ম:- (Even = জোড়, Odd = বিজোড়)

• Even + Even = Even (4+6 =20) (জোড়+জোড়=জোড়)
• Odd + Odd = Even (3+3=6)      (বিজোড়+বিজোড়=জোড়)
• Even + Odd = Odd (2+3=5)      (জোড়+বিজোড়=বিজোড়),
• Odd + Even = Odd (3+2=5)

আবার,

• জোড়+বিজোড়+বিজোড়= জোড়,
• বিজোড়+জোড়+জোড়=বিজোড়,
• বিজোড়+বিজোড়+বিজোড়=বিজোড়,
• জোড়+জোড়+জোড়=জোড়

# Even এবং Odd সংখ্যার, গুনের নিয়ম:- (Even = জোড়, Odd = বিজোড়)

• Even X Even = Even (2×2=4)
• Odd x Odd = Odd (3×5=15)
• Even X Odd = Even (2×3=6)
• Odd X Even = Even (3×2=6)

• The product of an even number of negative factors is positive. উদা-১: [(-1)(-1)=1]   উদা-২: [(-1)( -1)( -1)(-1)=1;
• The product of an odd number of negative factors is negative. উদা-১: ((-1)(-1)( -1)= -1; উদা-২: (-1)(-1) (-1)(-1) (-1)= -1]

গুনের চিহ্নগুলো-

ভাগের চিহ্নগুলো-

# Practice:

1. Arithmatic

Topics: Real Numbers:,|| Basic operations: Odd, Even,Mutiply,Division || Consecutive numbers || Factors, Multiples || Divisibility || Prime Numbers, || HCF and LCM

Topic: Number(সংখ্যা):

Digit (অঙ্ক / পাটিগণিতের প্রতীক): 0,1,2,3,4,5,6,7,8,9 (1,2,3,4,5,6,7,8,9 পর্যন্ত এই নয়টিকে বলা হয় সার্থক অঙ্ক)

Number (সংখ্যা / অঙ্কপাতন / দশ গুণোত্তর রীতি): Example- 543, 435 etc

স্থনীয় মান ও স্বকীয় মান এর পার্থক্যঃ

স্থনীয় মানঃ 346 সংখ্যাটিতে- 3 এর স্থানীয় মান 300, 4 এর স্থানীয় মান 40, 6 এর স্থানীয় মান 600। এভাবে করে লিখা হয়।

স্বকীয় মানঃ 346 সংখ্যাটিতে- 3 এর স্থানীয় মান 3 ই থাকবে, 4 এর স্থানীয় মান 4 ই থাকবে,63 এর স্থানীয় মান 6 ই থাকবে।

দেশীয় গণনা পদ্ধতি ও আন্তর্জাতিক গণনা পদ্ধতি এর সম্পর্কঃ ১ মিলিয়ন = ১০ লক্ষ। ১ বিলিয়ন = ১০০ কোটি।

দেশীয় গণনা পদ্ধতিঃ কোটি, নিযুত, লক্ষ, অযুত, হাজার, শতক, দশক, একক

আন্তর্জাতিক গণনা পদ্ধতিঃ

Worth to memorize: 1 mil- six zeroes, 1 bil- 9 zeroes, 1 trillion- 12 zeroes.

ক্যালকুলেশনের শর্টকাট নিয়ম জানতে হবে-

যেমন- 0.1×0.1=0.01

Topic: Real number(বাস্তব সংখ্যা):

• Integers(ইনটিজার)/Number System: Z = {…, -3, -2, -1, 0, 1, 2, 3, …}
• Whole numbers(পূর্ণ সংখ্যা): W = {0, 1, 2, 3, ..}
• Natural/Counting numbers(স্বাভাবিক সংখ্যা): N = {1, 2, 3, …}
• Consecutive number(ধারাবাহিক/ক্রমিক সংখ্যা): 1,2,3…বা 3,5,7,9…..etc
• Rational numbers(মূলদ সংখ্যা): Q = {-3, 0, -6, 5/6, 3.23} [যে numberগুলোকে fraction আকারে লিখা যায়]
• Irrational numbers(অমূলদ সংখ্যা): Q¯= {√2, -√6, π=3.14….} [যে numberগুলোকে fraction আকারে লিখা যায় না ও দুটি integer a ও b এর ratio আকারে লিখা যায় না]

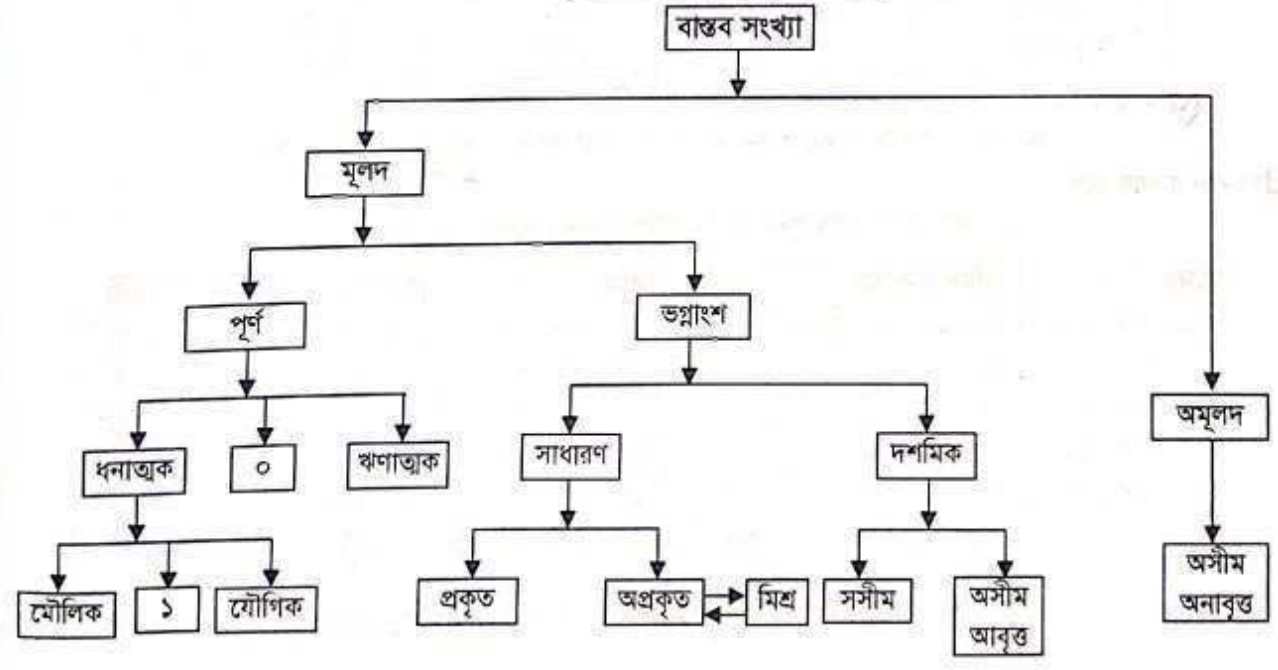
Integer(ইনটিজার): Z = {….-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…}

Positive, Negetive হতে পারে, কিন্তু Fraction(ভগ্নাংশ), Decimal(দশমিক সংখ্যা) সংখ্যা নয়। যেমন- 0, -2, 7 etc.

Zero: Integer, even number, Not +, Not – , non prime, non composite number, Zero is a multiple of every integers but is not a factor(the only number that zero can be a factor of is zero)

Non-Negative Integer: { 0, 1, 2, 3,………. }

Non-Positive Integer: {…….,- 3 , – 2 , – 1 , 0 }

Positive Numbers(ধনাত্মক সংখ্যা): {1,2,3,4,5,…..}

Negative Numbers(ঋণাত্মক সংখ্যা):  {…..,-4, -3, -2,-1}

positive + positive = positive. [6+3=9]
(negative) + (negative) = negative. [(-6)+(-2)= -8]

Positive × Positive = Positive [3×5 = 15]
Positive × Negative= Negative [(3x (-5) = -15]
Negative × Negative = Positive [-3) × (-5) = 15]

Positive ÷ Positive = Positive [6÷3 = 2]
Positive ÷ Negative= Negative [(6÷ (-3) = -2]
Negative ÷ Negative = Positive [(- (6) ÷ (-3) = 2]

* Positive বা Negative নাম্বার কে বর্গ(square) করলে positive নাম্বার-ই পাওয়া যায়।

* Negative Number এর কোনো root(বর্গমুল) নেই।

Whole Number(পূর্ণ সংখ্যা), W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10……}

Counting starts from 0 (It include natural numbers (that begin from 1 onwards), along with 0)

Natural/Counting Numbers (স্বাভাবিক সংখ্যা): N = {1, 2, 3, 4, 5, 6, 7, 8, 9,…}

Counting starts from 1

মূলদ সংখ্যা(Rational Number): হচ্ছে সেই সকল বাস্তব সংখ্যা যাদের  (ভগ্নাংশ) আকারে প্রকাশ করা যায়, যেখানে p এবং q উভয় পূর্ণ সংখ্যা, p ও q সহমৌলিক সংখ্যা এবং q≠0
*** সকল পূর্ণসংখ্যা, ভগ্নাংশ(+পৌনঃপুনিক বিশিষ্ট সংখ্যা)-ই মুলদ সংখ্যা। 

মূলদ সংখ্যা প্রকাশের প্রকারভেদ-

1. পূর্ণ সংখ্যা: যেমন- 3 বা 3/1 বা √9 , 12, 34 etc
2. ভগ্নাংশ[/Fractions]: (1.দশমিক[/Decimal], যেমন- , , ),
   (2.পৌনঃপুনিক[recurrent] দশমিক / সসীম দশমিক, যেমন- 5/3=1.666, ১.৬৩৬৩৬৩৬৩৬৩),
   (3.অনুপাত[/ratio],যেমন-  )

অমূলদ সংখ্যা(Irrational Number): যেসব বাস্তব সংখ্যাকে   (ভগ্নাংশ) আকারে প্রকাশ করা যায় না, তাদের অমূলদ সংখ্যা বলে। // যেসব বাস্তব সংখ্যা মূলদ সংখ্যা নয়, অর্থাৎ যাদেরকে দুইটি পূর্ণ সংখ্যার অনুপাত হিসেবে প্রকাশ করা যায় না তাদেরকে বলা হয় অমূলদ সংখ্যা। যেমন- =1.41421356237…, , π, e=2.71…., √9/7=3/√7 etc.
*** এরা অসীম অনাবৃত / পূর্নবর্গ নয় এরূপ যেকোনো সংখ্যার বর্গমুল বা বর্গমুলের ভগ্নাংশ-ই অমূলদ সংখ্যা। 

Topic: Consecutive number(ধারাবাহিক/ক্রমিক সংখ্যা):

যেকোনো নির্দিষ্ট ব্যবধান থাকে। এই ব্যবধান জোড়/বিজোড়/ধনাত্মক/ঋণাত্মক যেকোনো সংখ্যার ক্রমিক হতে পারে। যেমন-

even consecutive integer[ধারাবাহিক জোড় সংখ্যা/ ক্রমিক জোড়]:

• 2, 4, 6 (ব্যবধানঃ ২)
• -6,-8,-10 (ব্যবধানঃ ২) etc

odd consecutive integer[ধারাবাহিক বিজোড় সংখ্যা / ক্রমিক জোড়]:

• 1, 5, 3 (ব্যবধানঃ ২)
• 9, 11, 13 (ব্যবধানঃ ২)
• 21, 23, 25 (ব্যবধানঃ ২)
• 10,13,16 (বিজোড় ব্যবধানঃ ৩) etc

Positive consecutive (ধনাত্মক ক্রমিক): 1, 5, 3 (ব্যবধানঃ ২)

Negative consecutive (ঋণাত্মক ক্রমিক): -1, -5, -3 (ব্যবধানঃ ২)

# মনে রাখবে—

*** When each number is 1 greater than the previous number, then consecutive number formula: n, n+1, n+2, n+3……etc (ব্যবধানঃ ১)

ব্যবধান ১ আছে এরকম সিকোয়েন্সগুলো হচ্ছে:(n এর মান ইচ্ছেমত যেমন 1 বা 5 বসিয়ে চেক করতে পারবে)-

• (n, n+1, n+2) [এক্ষেত্রে, n=5 বসালে হয় 5x6x7]    এরকমভাবে (n+3).(n+4).(n+5), আবারো (n+4).(n+5)(n+6);..;…etc
• (n-1).n.(n+1)     [এক্ষেত্রে, n=5 বসালে হয় 4x5x6]
• (n-4).(n-3).(n-2) [এক্ষেত্রে, n=5 বসালে হয় 1x2x3]

*** When each number is 2 greater than the previous number, then consecutive number formula: n, n+2, n+4……etc (ব্যবধানঃ ২)

*** মনে রাখবে, তিনটি ক্রমিক স্বাভাবিক সংখ্যার গুণফল সর্বদাই ২ দ্বারা বিভাজ্য।
ব্যাখ্যাঃ তিনটি স্বাভাবিক ক্রমিক সংখ্যার মধ্যে কমপক্ষে একটি জোড় সংখ্যা থাকবেই। এজন্য তিনটি স্বাভাবিক ক্রমিক সংখ্যার গুণফল অবশ্যই ২ দ্বারা বিভাজ্য হবে। যেমন: তিনটি ক্রমিক সংখ্যা ৫, ৬, ৭ এদের গুণফল = ৫ × ৬ × ৭ = ২১০ যা ২ দ্বারা বিভাজ্য হয়।

*** একইভাবে, any three consecutive integers is divisible by 3! অর্থাৎ তিনটি ক্রমিক সংখ্যা ৩ দ্বারা বিভাজ্য হবে।

**** একইভাবে, তিনটি ক্রমিক সংখ্যার গুণফল সর্বদা 6 দ্বারা বিভাজ্য।
ব্যাখ্যাঃ n-এর জায়গায় যেকোনো স্বাভাবিক সংখ্যা বসালে, গুণফলটি 6 দ্বারা বিভাজ্য হবে।
গুণফল হবে = n(n + 1)(n + 2) = n³ + 3n² + 2n

**** একইভাবে, পাঁচটি ক্রমিক সংখ্যার গুণফল সর্বদা 20 দ্বারা বিভাজ্য।

——

আবার, তিনটি ক্রমিক জোড় সংখ্যার গুণফল/যোগফল ২, ৬ দ্বারা বিভাজ্য। [4,12,15 এগুলো নয়]

Practice:

# Question: If n is an integer greater than 6, which of the following must be divisible by 3?

A. n(n+1)(n−4)

B. n(n+2)(n−1)

C. n(n+3)(n−5)

D. n(n+4)(n−2)

E. n(n+5)(n−6)

Solution1:

আমরা জানি, any three consecutive integers is divisible by 3! অর্থাৎ তিনটি ক্রমিক সংখ্যা ৩ দ্বারা বিভাজ্য(divisible)।

৩ সংখ্যার ক্রমিক প্যাটার্ন গুলো হচ্ছেঃ n.(n+1).(n+2), (n+2)(n+3)(n+4),….. etc অথবা (n-1).n.(n+1), (n−7)(n−6)(n−5),….. etc যেকোনো কিছু।
{কেননা n এর যেকোনো মান যেমন n=5 বসিয়ে n.(n+1).(n+2)=5x6x7 যা একটি ক্রমিক সংখ্যা, (n+2)(n+3)(n+4)=7x8x9 যা একটি ক্রমিক সংখ্যা….etc।
একইভাবে, n=5 বসিয়ে (n-1).n.(n+1)=4x5x6 যা একটি ক্রমিক সংখ্যা, (n−7)(n−6)(n−5) = -2 x -1 x 0 যা একটি ক্রমিক সংখ্যা……etc}
আর, ক্রমিক প্যাটার্ন জোড়া গুলোর মধ্যে অবস্থানের মানের পরিবর্তন করলেও ৩ দ্বারা বিভাজ্য(divisible) হয়। যেমন- 5x6x7 এর 5 এর জায়গায় 7 বসালেও 3 দ্বারা বিভাজ্য(divisible) হয়।

ক্রমিক প্যাটার্ন সহজে বুঝতে এই ছক দেখতে পার- (n−7)(n−6)(n−5)(n−4)(n−3)(n−2)(n−1)n(n+1)(n+2)(n+3)(n+4)(n+5)(n+6) 

এক্ষেত্রে,প্যাটার্নগুলাতে (n-1) বা (n+2) বা (n−4) একই জিনিস বলা যায়, কারণ তারা এরা প্রত্যেকেই তাদের ক্রমিক জোড়া গুলোর প্রথম পার্ট।

তো প্রশ্ন থেকে দেখাই যাচ্ছে, (n−4).n.(n+1) হচ্ছে একটি ক্রমিক সংখ্যা প্যাটার্ন, আর আমরা জানি-তিনটি ক্রমিক সংখ্যা ৩ দ্বারা বিভাজ্য(divisible)। তাই অপশন A ই হবে নির্ণেয় উত্তর।

If we have 3 consecutive numbers such as n, (n+1), (n+2), we know for sure that at least one of them is divisible by 3.
given numbers such as (n-1)*n*(n+1), we know that the product is divisible by 3.

# Solution2:

3 দ্বারা ভাগ যেতে হবে এমন, n এর মান যা 6 থেকে বড় সংখ্যাগুলা Test করি। তাই, 7 ও 8 বসিয়ে value গুলো test করি-

A. n (n+1) (n-4) = 7*8*3 and if n = 8 –> 8*9*4
B. n (n+2) (n-1) = 7*9*6 and if n = 8 –> 8*10*7
C. n (n+3) (n-5) = 7*10*5; eliminate as there are no multiples of 3
D. n (n+4) (n-2) = 7*11*5; eliminate as there are no multiples of 3
E. n (n+5) (n-6) = 7*12*1 and and if n = 8 –> 8*13*2

দেখা যাচ্ছে, only A তে 3 দ্বারা divisible হয়, তাই A ই হচ্ছে answer.

# (all solution link) The product of 3 numbers to be divisible by 3 at least one of them must be divisible by 3. So, to ensure that the product of 3 integers shown is divisible by 3 all 3 numbers must have different remainders upon division by 3, meaning that one of them should have remainder of 1, another reminder of 2 and the last one remainder of 0, so be divisible by 3. We should have something like n(n+1)(n+2) (for example: if n divided by 3 yields remainder of 1, then n+1 yields remainder of 2 and n+2 yields remainder of 0, thus it’s divisible by 3 OR if n divided by 3 yields remainder of 2, then n+2 yields remainder of 1 and n+1 yields remainder of 0, thus it’s divisible by 3).

Only option A satisfies this, because n(n+1)(n−4)=n(n+1)(n−6+2) and n−6n−6 has the same remainder as nn upon division by 3 thus we can replace it by nn.

Answer: A.

#

Shortcut: In every set of 3 consecutive numbers, ONE of them must be divisible by 3 when we are multiplying each of the digits

1*2*3
2*3*4
3*4*5
4*5*6

(A) n(n + 1)(n – 4)

The easiest is if we have something like n(n+1)(n+2)
We know in this case we DEFINITELY have an expression that is divisible by 3.
n=1 => 1*2*3
n=2 => 2*3*4
n=3 => 3*4*5

All are divisible by 3.

Any expression must pass our 3 consecutive integer test.

n(n + 1)(n – 4)
n=1 => 1*2*-3
n=2 => 2*3*1
n=3 => 3*4*-1

Even if n = 4 we have:
4*5*0 = 0 which is divisible by 3.

If n = 16
16*17*12 is divisible by 3.

So (A) passes all the tests and one of numbers in the expression will be divisible by 3 so the whole expression when multiplied together will be divisible by 3.

Question: If a, b, c are three consecutive positive even integers, which of the following must be an integer?

I. (a+b+c)/2
II.(a+b+c)/4
III. (a+b+c)/6

A. I only
B. III only
C. I and II only
D. I and III only
E. I, II and III

Solutions:

Key concept: All EVEN integers can be rewritten as 2n (where n is some integer)
Aside: This also means that all ODD integers can be rewritten as 2n + 1 (where n is some integer)

If, a, b, c are consecutive even integers.
Then, the even positive integers be 2n , 2n+2 & 2n+4 (where, three consecutive numbers be x, x+2, x+4)

(((so,
a=2n
b=2n+2
c=2n+4
a+b+c = 2n+(2n+2)+(2n+4) = 6n+6 )))

I. (a+b+c)/2  =2n+2n+2+2n+4/2 = 6n+6/2 = 3n+3  [if n is an integer, then 3n+3 must also be an integer.]
II. (a+b+c)/4 =2n+2n+2+2n+4/4 = 6n+6/4= 3n+3  [If n=2, then 3n+3/2=3(2)+3/2=9/2 is NOT an integer]
III. (a+b+c)/6=2n+2n+2+2n+4/6 = 6n+6/6 = n+1  [if n is an integer, then n+1 must also be an integer.]

Hence, Answer must be I. & III, (D)

Question:

Solution: even positive integers be 2n , 2n+2 & 2n+4

কিছুক্ষেত্রে যেমন- n = 2 বসালে, a+b+c = 4+6+8 = 18

তখন, 18 কে 4, 12, 15 দিয়ে ভাগ যাবে না। তাই ওইগুলো answer হবে না।

সাজেশনঃ প্রশ্নে Must be বলেছে নাকি could be বলেছে ঐটা খেয়াল রাখবে।

#

#

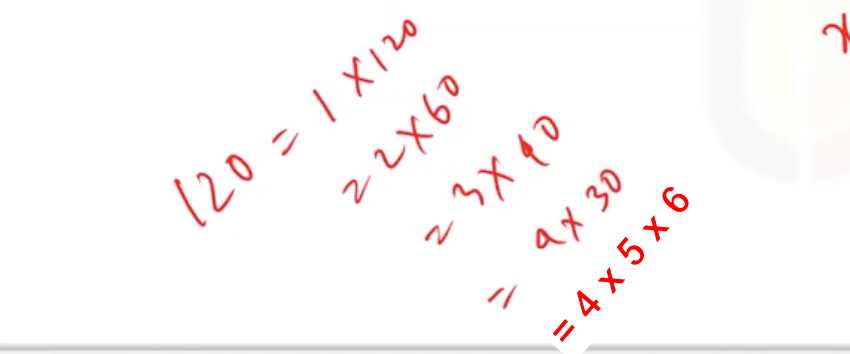
Topic: Divisibility

Division(ভাগ):

# Dividend =  Quotient x Divisor + Reminder

অর্থাৎ, ভাজ্য(p) = ভাগফল(q) x ভাজক(k) + ভাগশেষ(r)

*** If the remainder is r when p is divided by k then it can be written, p=kq + r where q is an integer.

# Dividend/Divisor = Quotient + (Reminder/Divisor)

অর্থাৎ, (ভাজ্য / ভাজক) = ভাগফল + (ভাগশেষ/ভাজক)

 

Practice:

Q# ভাজক 10, ভাগফল ১০ এবং ভাগশেষ 1 হলে, ভাজ্য কত?

Solution: আমরা জানি, ভাজ্য(p) = ভাগফল(q) x ভাজক(k) + ভাগশেষ(r)

∴ ভাজ্য(p) = 10  x 10 + 1 = 101 Ans.

#

#

*** odd সংখ্যক divisor বের করার ট্রিকস- ওই number এর square value……

# শর্টকাট ভাগ করার নিয়ম-

৫ দিয়ে শর্টকাট ভাগ করার নিয়ম:

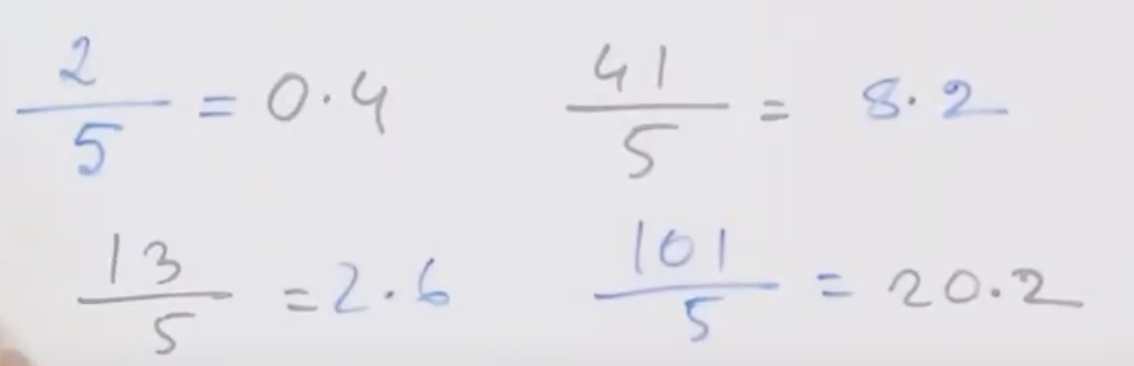
২৫ দ্বারা –

 

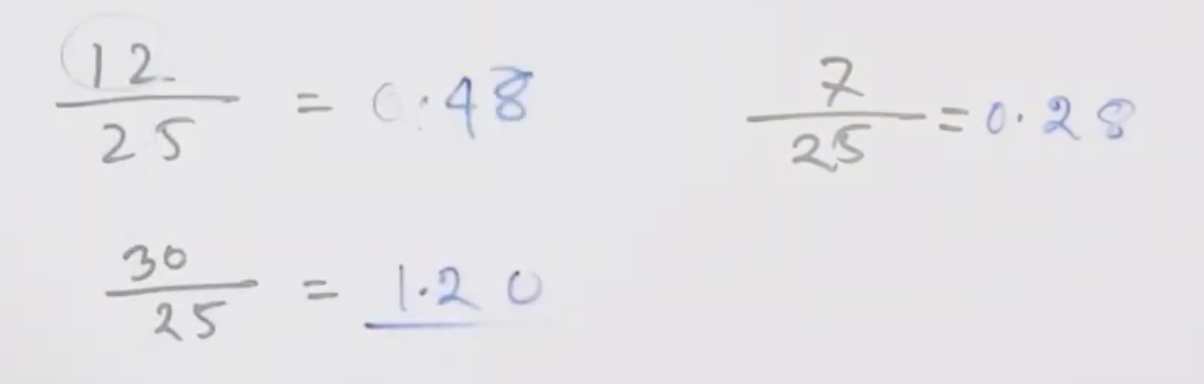
Divisible:

Divisible (নিঃশেষে বিভাজ্য): একটি সংখ্যাকে আরেকটি সংখ্যা দ্বারা নিঃশেষে ভাগ করা গেলে[ভাগশেষ থাকবেনা] । যেমন- 39 সংখ্যাটি 13 দ্বারা বিভাজ্য।

Exact Divisibility by 2: 2 divide all even numbers exactly such as 2, 4, 6, 8, 12, 14, 16, 18, 20, etc. We see that the unit digit of these numbers is 0, 2, 4, 6 or 8.

The product of 2 and a whole number is called an even number.

A number is exactly divisible by 2 it its unit digit is 0, 2, 4 6 or 8.

Divisibiility rules: 2,4,5 || 3,6,9 ||

• i) কোন সংখ্যার একক স্থানীয় অংকটি শূন্য হলে অথবা জোড় সংখ্যা হলে, প্রদত্ত সংখ্যাটি ২ দ্বারা বিভাজ্য। অর্থাৎ,
  একটি integer 2 দিয়ে divisible হবে যদি integer এর শেষ সংখ্যা(units digit)টি even or 0 হয়। যেমন- 598 integer টি 2
  দিয়ে divisible.
• ii) একটি integer 3 দিয়ে divisible হবে যদি integer এর digit গুলোর sum 3 দিয়ে divisible(নিঃশেষে বিভাজ্য) হয়. যেমন : 2145 integer টি 3 দিয়ে divisible কেননা 2 + 1 + 4 + 5 = 12 এবং 12 integer টি 3 দিয়ে divisible.
• iii) একটি integer 4 দিয়ে divisible হবে যদি integer টির শেষ দুটি ডিজিট 4 দ্বারা বিভাজ্য হয়(/শেষ দুটি ডিজিট 00 হলেও) 4 দ্বারা বিভাজ্য। যেমন: 440 সংখ্যাটির শেষ দুটি সংখ্যা 40, যাকে 4 দ্বারা ভাগ(divisible) করা যায়। অন্যভাবে 440 integer টি 4 দিয়ে divisible কেননা 40 integer টি 4 দিয়ে divisible.
• iv) একটি integer 5 দিয়ে divisible হবে যদি তার শেষ সংখ্যা(units digit)টি 0 বা 5 হয়। যেমন : 1115
• vii) একটি integer 6 দিয়ে divisible হবে যদি integer টি 2 ও 3 উভয়কে দিয়ে divisible হয়। বিকল্প সহজ নিয়মঃ জোড় সংখ্যা ও একই সাথে sum 3 দিয়ে divisible(নিঃশেষে বিভাজ্য) হলে।
  • Example: For 123456,
  • Split the number into groups of three digits, 123 & 456.
  • 123−456=−333; if -333 is divisible by 7, so is the original number.
    (আরও বড় সংখ্যা হলে সেক্ষেত্রে, জোড় three digits গুলো থেকে বিজোড় three digits গুলোকে বিয়োগ করে এরপর 7 দ্বারা ভাগ করব) সবচেয়ে সহজ নিয়ম- https://youtu.be/17nXsZqEOTM?si=A4oHy3YsL_RKVBTZvii) একটি integer 7 দিয়ে divisible কিনা তা দুইভাবে বের করা যায়-
    1. Subtract Method (Basic Method for small Numbers): শেষ সংখ্যাতে ডবল করলে যা হয় সেটা মুল সংখ্যারর শেষ সংখ্যা ব্যাতিত বাকি সংখ্যা থেকে বিয়োগ দেব, এরপর ৭ দ্বারা ভাগ করব। (বড় সংখ্যা হলে পর্যায়ক্রমে এভাবে করতে থাকব।)
    • Example: For 826
    • Double the last digit 6→12
    • Subtract 82−12=70, which is divisible by 7.
      

    2. Forming Groups of Three Method (Advanced Method for Large Numbers):

• viii) একটি integer 8 দিয়ে divisible হবে যদি ডান দিকের তিনটি digit এর integerটি ৪ দিয়ে divisible হয় ।
  যেমন- 44816 integerটি 8 দিয়ে divisible. কেননা 816 integerটি 8 দিয়ে divisible.
• ix) একটি integer 9 দিয়ে divisible হবে যদি sum of the digits 9 দিয়ে divisible হয়।
  12339 integerটি 9 দিয়ে divisible কেননা 1+2+3+3+9 = 18 integerটি 9 দিয়ে divisible.
• xiii) একটি integer 10 দিয়ে divisible হবে যদি এর units digit 0 হয়।
• ix) একটি integer 11 দিয়ে divisible হবে যদি ডান দিক থেকে odd numbered place গুলোর sum of the digit এবং even numbered place গুলোর sum of the digit এর পার্থক্য 0 বা 11 দ্বারা divisible হয়।
  যেমন- 411213 integer টি 11 দিয়ে divisible কেননা (1+2+3)-(4+1+1)=0 Divisor এর divisibility rule মানে না এমন কোনো Dividend নেই যা evenly divisible.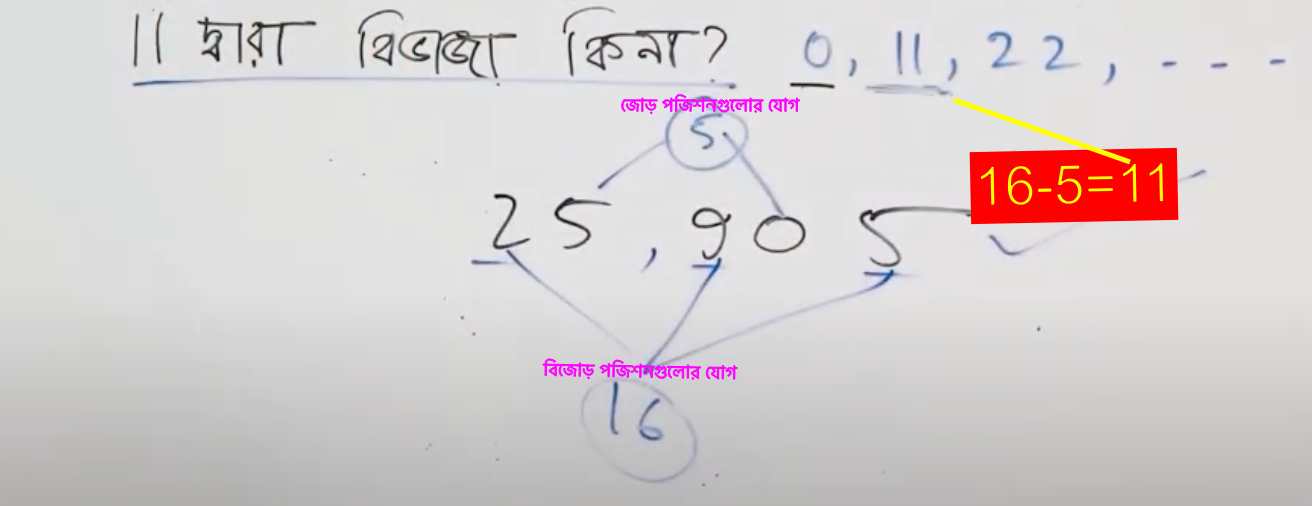
• একটি সংখ্যাকে ১২ দ্বারা divisible করা যাবে যদি তাকে ৩ ও ৪ উভয় সংখ্যা দ্বারা divisible করা যায়।
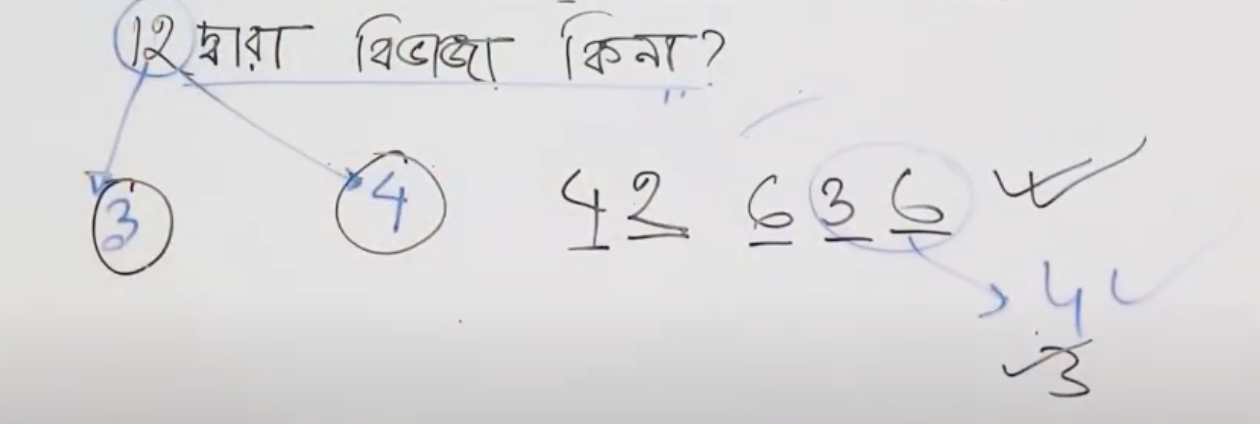
• Divisibility By 13: শেষ সংখ্যাতে 4গুণ করলে যা হয় সেটা মুল সংখ্যারর শেষ সংখ্যা ব্যাতিত বাকি সংখ্যা থেকে বিয়োগ দেব, এরপর 13 দ্বারা ভাগ করব। (বড় সংখ্যা হলে পর্যায়ক্রমে এভাবে করতে থাকব।)
• Divisibility By 14: A number is divisible by 14, if it is divisible by 2 as well as 7.12.
• Divisibility By 15: A number is divisible by 15, if it is divisible by both 3 and 13.
• Divisibility By 16: A number is divisible by 16, if the number formed by the last 4 digits is divisible by 16. Ex. 7957536 is divisible by 16, since the number formed by the last four digits is 7536, which is divisible by 16.
• Divisibility By 17:
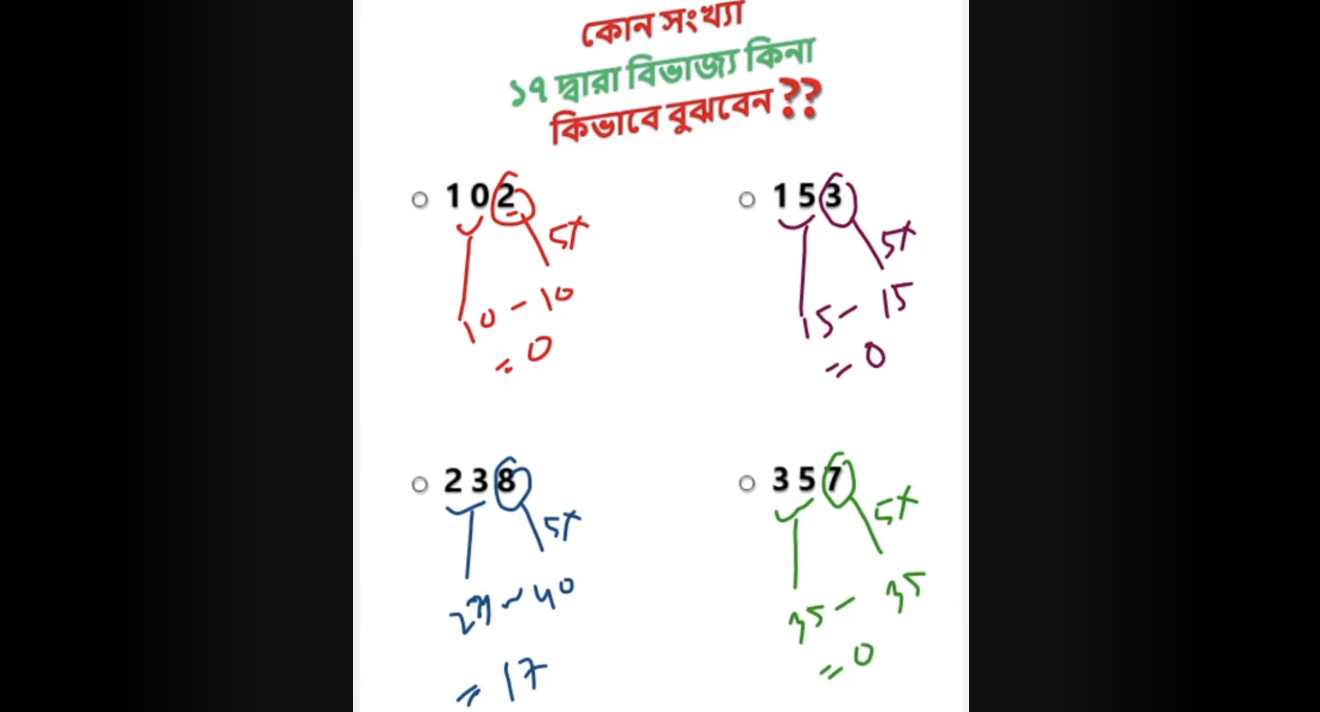  Divisibility By 19:
  Divisibility By 24: A given number is divisible by 24, if it is divisible by both 3 and 8.Divisibility By 25: শেষ দুই ঘর ২৫ দ্বারা বিভাজ্য হলে।Divisibility By 40: A given number is divisible by 40, if it is divisible by both 5 and 8.Divisibility By 80: A given number is divisible by 80, if it is divisible by both 5 and 16.
  Note: If a number is divisible by p as well as q, where p and q are co-primes, then the given number is divisible by pq.
  If p and q are not co-primes, then the given number need not be divisible by pq, even when it is divisible by both p and q.
  Ex. 36 is divisible by both 4 and 6, but it is’ not divisible by (4 x 6) = 24, since
  4 and 6 are not co-primes.

Divisibility র এই সব rule এর উপর ভিত্তি করে কোন integer বড় অন্য কোন divisor দিয়ে divisible কিনা তা নির্ণয় করতে হবে।

*** Each number is divisible by its factors; so factors are also called divisors(ভাজক)।  [ভাজক(divisor) সংখ্যা বের করার অর্থ হলো প্রদত্ত সংখ্যাটিকে মোট কয়টি সংখ্যা দ্বারা ভাগ করা যায়]

কত দ্বারা বিভাজ্য ? ।। Divisibility ।। Number System ।in Bengali।। কোন সংখ্যা দ্বারা বিভাজ্য

*** তিন দ্বারা বিভাজ্য তিন অঙ্কের প্রথম সংখ্যাটি হবে = 102. কারণ, 102 এর অঙ্কগুলি যোগ করলে যোগফল হবে = 1 + 0 + 2 = 3, যা তিন দ্বারা বিভাজ্য এবং তিন অঙ্কের প্রথম সংখ্যা।

*** তিন অঙ্কের ক্ষুদ্রতম সংখ্যা = 100.

# প্রাকটিসঃ-

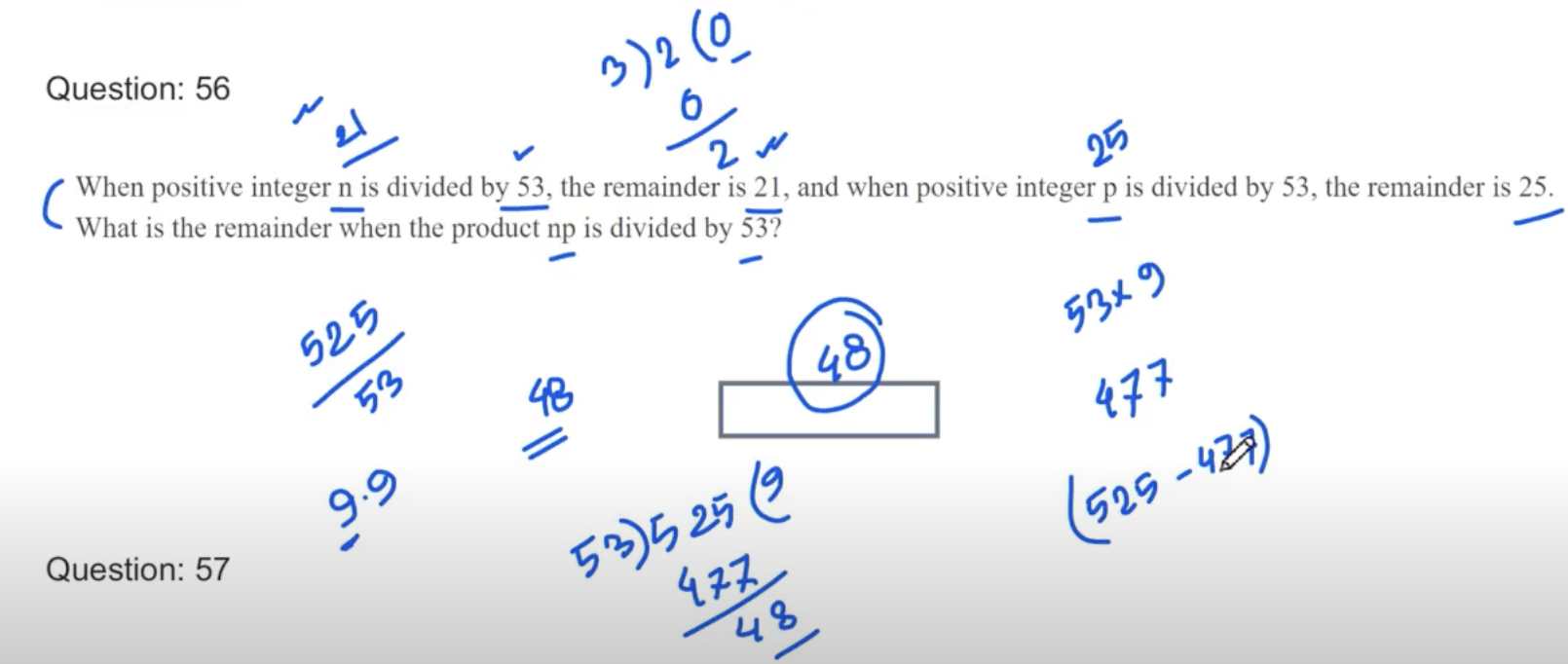
# ৫০ থেকে ১০০ এর মধ্যে ২ দ্বারা বিভাজ্য সংখ্যা কয়টি?

শর্টকাট নিয়ম-
১মে, ২ দ্বারা প্রত্যেকটা সংখ্যাকে ভাগ করব।
৫০/২ = ২৫
১০০/২ = ৫০
২য়ত, এদের বিয়োগ করব।
৫০ – ২৫ = ২৫
৩য়ত, প্রশ্নে দেয়া ছোট সংখ্যাটার দিকে লক্ষ করব যে, এটি নিঃশেষে ভাগ করা গেসে কিনা। নিঃশেষে ভাগ করা গেলে এটির সাথে ১ যোগ করে দেব।
২৫ + ১ = 26

# ১০০ থেকে ২০০ এর মধ্যে৩ দ্বারা বিভাজ্য সংখ্যা কয়টি?

আরও টেকনিক খাটিয়ে, ২০০ – ১০০ = ১০০,   ১০০/৩ = ৩৩.৩৪ = ৩৩

শর্টকাট নিয়ম-
১মে, ২ দ্বারা প্রত্যেকটা সংখ্যাকে ভাগ করব।
১০০/৩ = ৩৩.৩৩
২০০/৩ = ৬৬.৬৬
২য়ত, এদের বিয়োগ করব।
৬৬.৬৬ – ৩৩.৩৩ = ৩৩.৩৩
৩য়ত, প্রশ্নে দেয়া ছোট সংখ্যাটার দিকে লক্ষ করব যে, এটি নিঃশেষে ভাগ করা গেসে কিনা। যদি নিঃশেষে ভাগ করা যেত এটির সাথে ১ যোগ করে দেয়া হত।

 

ক্রমিক সংখ্যার যোগফল – শর্টকাট পদ্ধতি ( দ্বিতীয় অংশ)

UNIT DIGIT + ভাগশেষ নির্ণয়(Find Remainder) /Number System:

UNIT DIGIT নির্ণয় সবথেকে সহজ নিয়মেঃ 

x = x¹ x² x³ x⁴

2 = 2 4 8 6

3 = 3 9 7 1

4 = 4, 6

• 5=5
• 6 = 6

7 = 7 9 3 1

8 = 8 4 2 6

9 = 9 1

video link-  UNIT DIGIT TRICKS | NS CAREER ACADEMY

ভাগশেষ নির্ণয়- 

Power Even = 1 (Reminder)

Power Odd = base

#

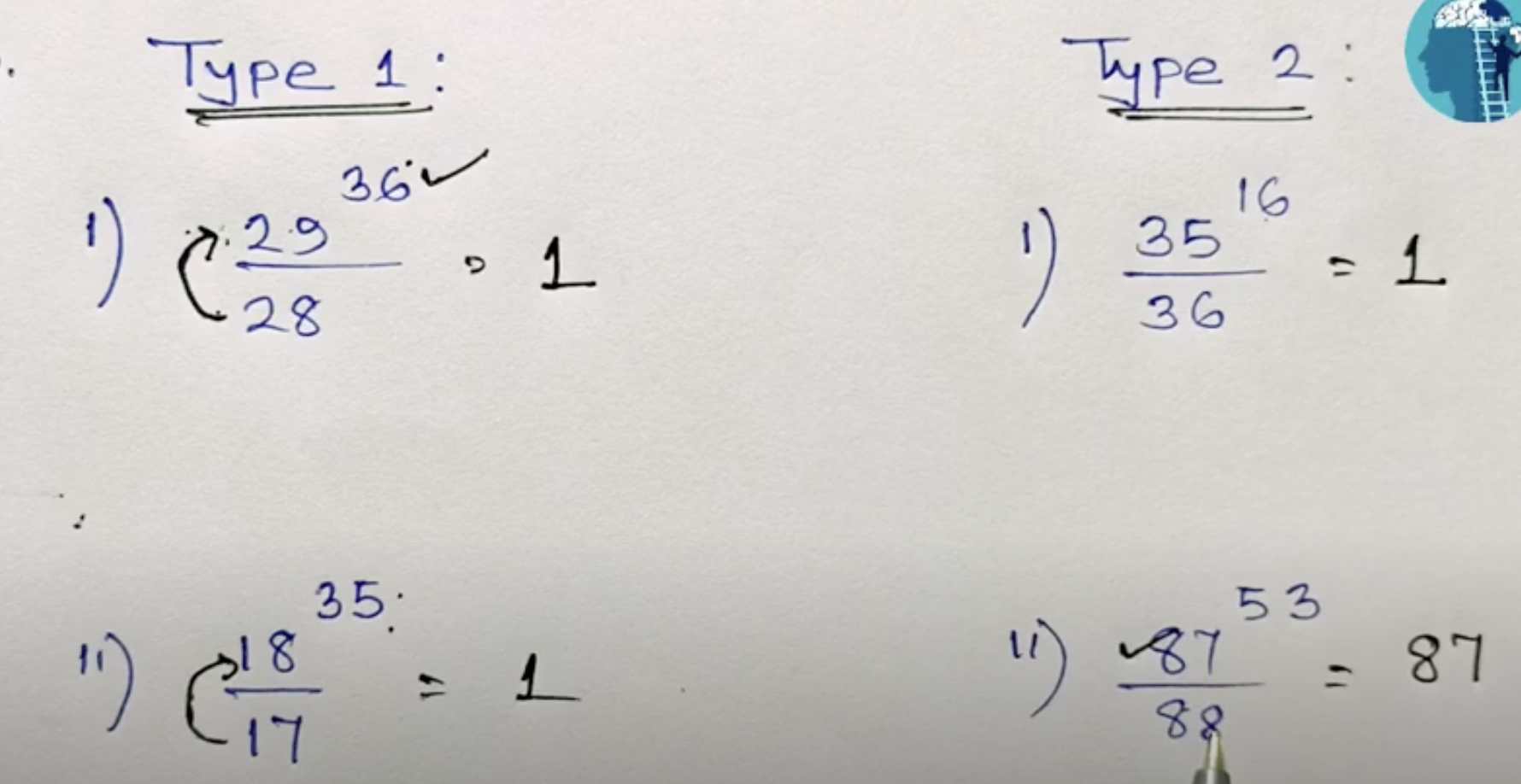
ভাগশেষ নির্ণয় ( Find Remainder )

Remainder Tricks |Remainder finding | অবশিষ্ট নির্ণয় | Remainder theorem in Bengali | SSCE |

ভাগশেষ নির্ণয় করার সহজ পদ্ধতি । How to Find Remainder in Division ? [ Bengali ] | Number System

Practice:

 

 Factor/Factorisation (গুণনীয়ক/উৎপাদক/ভাজকের সংখ্যা):

একটি সংখ্যাকে যে সকল সংখ্যা দ্বারা নিঃশেষে ভাগ করা যায় সেসব সংখ্যাকে Factor বলে।

* 1 হচ্ছে সব নাম্বার এরই common factor.

* (0 এবং 1 ব্যতীত) প্রতিটি সংখ্যার কমপক্ষে দুটি গুণনীয়ক(factor) রয়েছে, একটি হল 1(সবসময়) এবং বাকি সংখ্যাটি হল ঐ সংখ্যাটিই(নিজেই)।

যেমন-

পদ্ধতি ১ঃ #

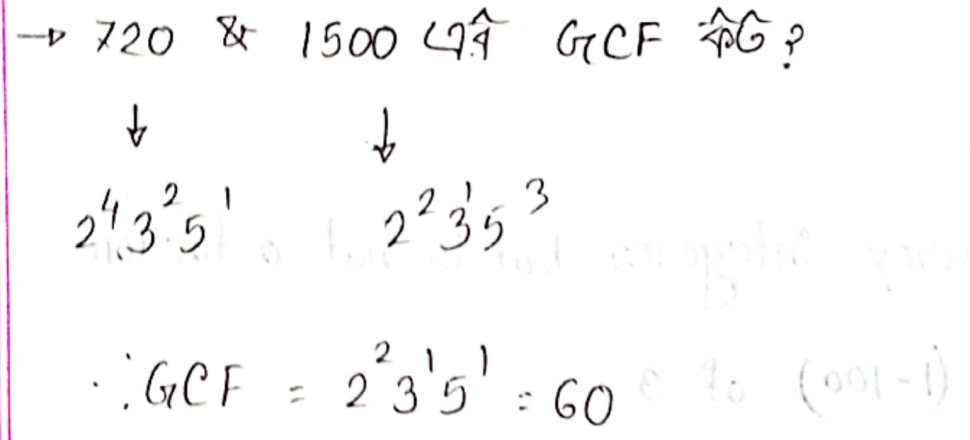
পদ্ধতি 2ঃ(অন্যভাবে)

Q: 12 ও 16 এর G.C.F কত?

The factors of 12 = 1, 2, 3, 4, 6, 12 এগুলো (৬টি)

The factors of 16 = 1, 2, 4, 8, 16 এগুলো (৫টি)

The common factors of 12 & 16 = 1, 2, 4 এগুলো (৩টি)

Highest Common Factor(H.C.F.) বা Gretest Common Factor(G.C.F) বা (G.C.M.) বা (G.C.D.) বা [গ.সা.গু.]:

The Highest Common Factor (H.C.F.) of 12 & 16  = 4

shortcut: 12=3¹x2²,  16 = 2⁴;    12 & 16 = 2²=4 (শর্টকাটঃ G.C.F এ শুধু কমন পাওয়ার এর সবচেয়ে কম সংখ্যক নেব)

পদ্ধতি 3ঃ (গ.সা.গু নির্ণয়ে শর্টকাট পদ্ধতি) –link2– [ছোট সংখ্যাগুলোর ক্ষেত্রে এটা বেস্ট ট্রিক্সস]

# মনে রাখবে. গ.সা.গু এর সর্বোচ্চ মান হতে পারে সবকটি এর সবচেয়ে ছোট সংখ্যার সমান বা ছোট। যেমন- 4,8,36, 630 এই এর মান হতে পারে 4 বা এর ছোট(সর্বনিম্ন 1)।

# সংখ্যাগুলো বেশি হলে- সবচেয়ে ছোট সংখ্যা বাছাই করব, ছোট সংখ্যাটির ডিরেক্ট গুণিতক বড় সংখ্যায় পাওয়া গেলে ঐটি ডিরেক্ট বাদ। এভাবে না মিললে next testing হবে- সবচেয়ে ছোট সংখ্যাটিকে devide করে করে দেখব, যাতে ছোট সংখ্যাটির devideকৃত মানটি(সংখ্যাটি) দিয়ে হলেও যেন বাকি সংখ্যাগুলো গুণিতক করা যায়, তাহলে ঐ(সংখ্যা)টিই গ.সা.গু।

অথবা, সবকটি সংখ্যাকে যে সংখ্যা দ্বারা devide করা যায় ঐটিই গ.সা.গু। (সবকটি সংখ্যার মধ্যে ন্যূনতম দুটি সংখ্যাকে devide করা না গেলে 1 ই হবে গ.সা.গু।
devide করার ক্ষেত্রে, যতবার devide করা যাবে ততবার ঐ সংখ্যা(গুলো) note করে লিখে রাখব, note করে রাখা সংখ্যাগুলো গুণ করলেই ঐটিই গ.সা.গু।

উদাহরণ- 

# 5, 10 এর গ.সা.গু নির্ণয় কর।

5/10 (5)= (বা, 5/5, 10/5) এক্ষেত্রে= 5

# 12, 28 এর গ.সা.গু নির্ণয় কর।

12/28 (2) = 6/14 [2] = 3/7 (বা, 12/12, 28/2) এক্ষেত্রে= 2 x 2 = 4

# 20, 25, 30 এর গ.সা.গু নির্ণয় কর।

20/4 = 5 [সবচেয়ে ছোট সংখ্যাটির devide মান 5, যা বাকি সংখ্যাগুলোরও গুণিতক হয়। এজন্য এটাই নির্ণেয় গ.সা.গু]

#

Prime Factorisation(মৌলিক গুণনীয়ক):

যে সংখ্যাকে ১ও ঐ সংখ্যা ছাড়া অন্য কোন সংখ্যা দ্বারা নিঃশেষে বিভাজ্য হয় না তাকে মৌলিক গুণনীয়ক বলে।যেমন- 5 সংখ্যাটি এক ও 5 ছাড়া অন্য কোন সংখ্যা দ্বারা নিঃশেষে বিভাজ্য হয় না।

# 350 এর unique dna = 2¹5²7¹ (350 = 2x5x5x7)

তাহলে দেখা যাচ্ছে, 350 এর Prime Factor = 2, 5, 7

এবং 350 এর মোট factor = (1+1) x (2+1) x (1+1) = 12 টি

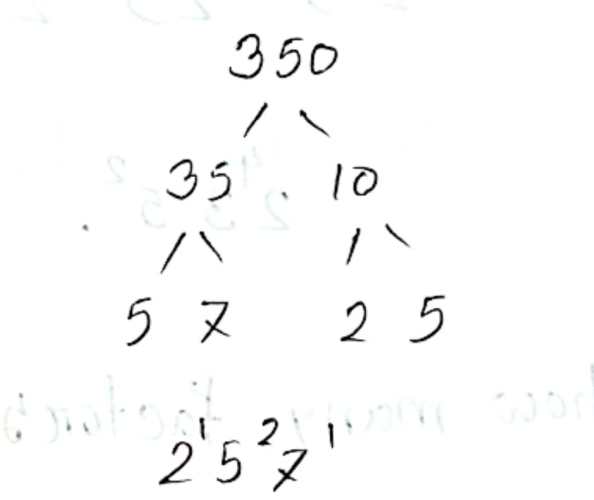
বা,

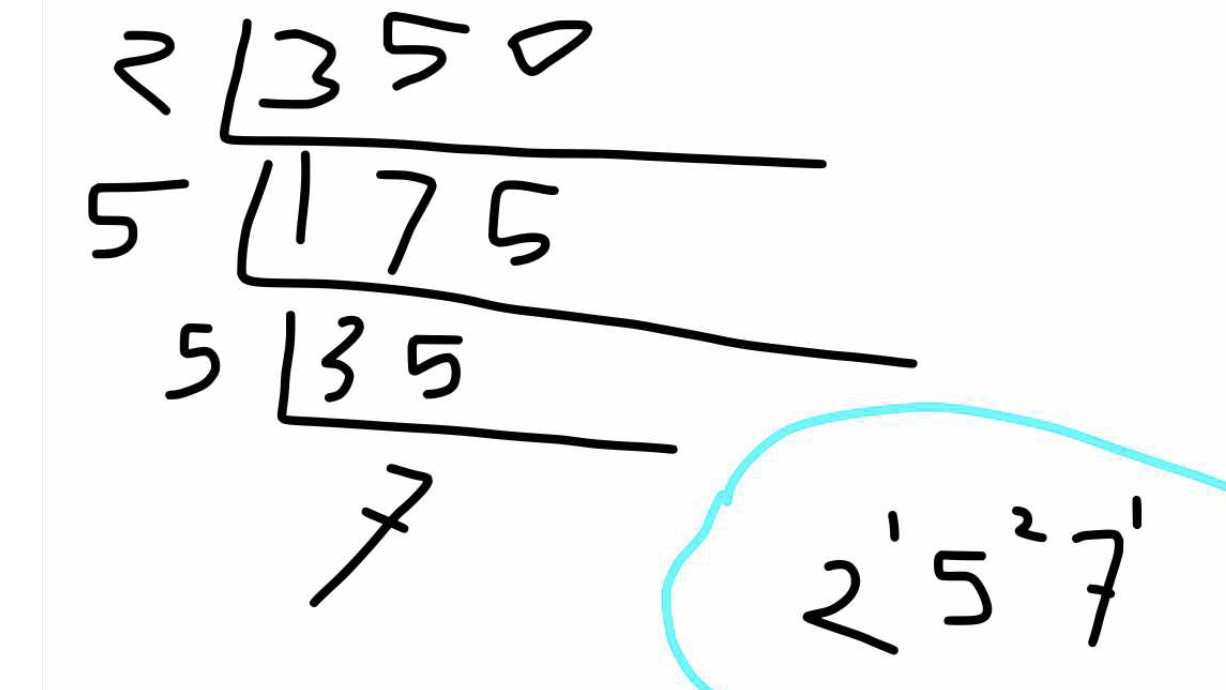
total factors(number) বের করার উপায়: unique dna এর প্রতিটি ঘাতের সাথে 1 যোগ করে সেগুলো গুণ করলে total factor numbers পাওয়া যায়।

Q: how many factor(numbers) of 350?

Ans: 350 এর unique dna = 2¹5²7¹ (350 = 2x5x5x7)

তাহলে দেখা যাচ্ছে, 350 এর মোট factor = (1+1) x (2+1) x (1+1) = 12 টি

 

Multiples(গুণিতক/গুনের নামটা):

এটি Factor এর বিপরীত। কোন সংখ্যাকে পূর্ণ সংখ্যা দিয়ে গুণ করলে যে গুণফল সংখ্যা পাওয়া যায়, তাকে ঐ সংখ্যার গুণিতক বলে।

* Zero is a multiple of every integers but is not a factor(the only number that zero can be a factor of is zero)

* Factor are not infinite, but multiples are infinite.

Least Common Multiple (L.C.M.) [ল.সা.গু]:

পদ্ধতি ১ঃ যেমন-

Q: 12 ও 16 এর L.C.M. বের কর। 

The multiples of 12 = 12, 24, 36, 48, 60, 72, 84, 96…144…192

The multiples of 16 = 16, 32, 48, 64, 80, 96, 112….144…192

The common multiples of 12 & 16 = 18, 96, 144, 192.

The Least Common Multiple (L.C.M.) of 12 and 16 = 48

shortcut: 12=3¹x2²,  16 = 2⁴;    12 & 16 = 2⁴x3¹=48 (শর্টকাটঃ L.C.M এ এভারেজ সবগুলো থেকে পাওয়ার এর সবচেয়ে বেশি সংখ্যক নেব)

পদ্ধতি ২ঃ(অন্যভাবে)

পদ্ধতি ৩ঃ 

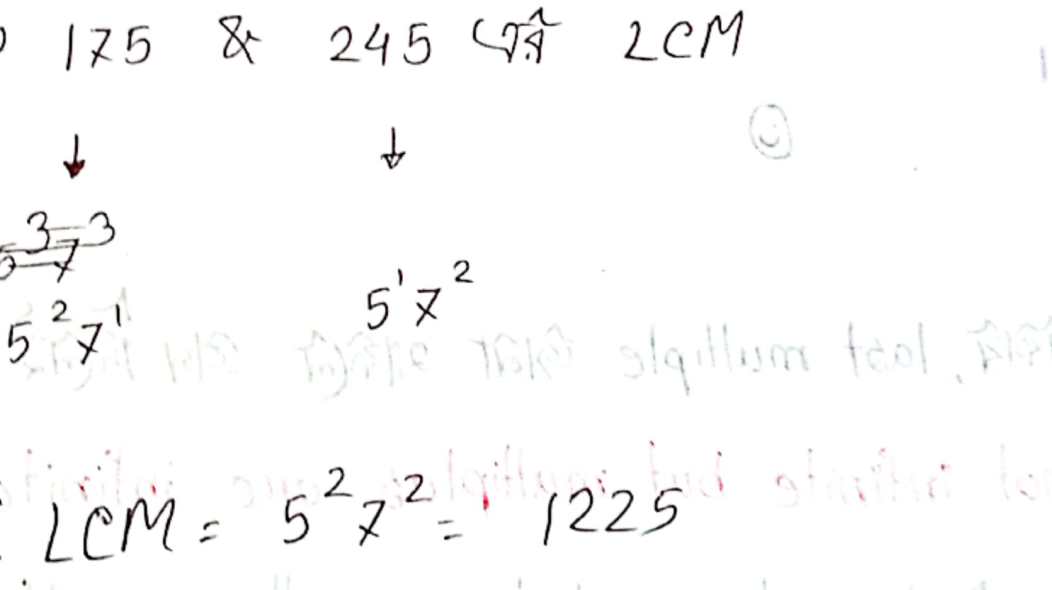
total multiples(number) বের করার উপায়:

Q: how many Multiple(numbers) in (1-100) of 3?

Ans: {(last multiple – first multiple)/3} + 1

{(99-3)/3} + 1 = 33

শর্টকাট: (last Multiple জানা থাকলে ভাগ দিলেই হয়, 99/3=33)

আরও একটি উদাহরণ: how many Multiple(numbers) in (1-100) of 3?

Ans: 100/4=25 (শর্টকাট)

Practice:

#

or, and এগুলোর দুইটার দুই meaning.

• or দ্বারা A U B কে বোঝায়। অর্থাৎ either A or B.  ((( U হচ্ছে  or [অথবা] )))
•  and দ্বারা A∩B অর্থাৎ Both কে বোঝায়।

সুত্রঃ A U B = A + B – A∩B

1-100 এর মধ্যে: A∩B অর্থাৎ 3×4=12 আছে 8 টি। এবং A∩B অর্থাৎ 4×5=20 আছে 8 টি।

# কিছু সূত্রঃ

#* if you divide an integere x by anothere integer y, the result is another integer, then; y is a factor of x.

# 9! = 9 x 8!

# how to find number of factors / sum of factors / উৎপাদকের সংখ‍্যা নির্ণয়/ product of factors/bengali (All typel)

# কোন একটা সংখ্যার বেজোড় সংখ্যক ফ্যাক্টর থাকলে বলা হলে, তাহলে বুঝে নেব তা হবে কোন একটা সংখ্যার স্কয়ার। যেমন- 4 এর বেজোড় সংখ্যক ফ্যাক্টর আছে = 1,2,4

যেমন-

# দুটি সংখ্যার গুণফল = সংখ্যাদ্বয়ের গ.সা.গু(H.C.F) x সংখ্যাদ্বয়ের ল.সা.গু(L.C.M)

অর্থাৎ, LCM x HCF = a x b বা, If the HCF of a and b = x, and the LCM of a and b = y Then, ab = xy

Example:  a=4, b=5,

The HCF of 4 & 5 is = 1.

The LCM of 4 & 5 = 20.

So,

R.H.S = 4 × 5 = 20,

L.H.S = LCM x HCF = 20 × 1 = 20

(proved)

# Multiple of ratio x H.C.F = L.C.M

So, 3x4x4 = 48

 

1. * If a number N is divisible by a number x, then N is also divisible by all factors of x.
Example: 32 is divisible by 16. Therefore, 32 must be divisible by 1, 2, 4, 8 which are all factors of 16.

02. কিছু সংখ্যার H.C.F বের করার ক্ষেত্রে একটি সংখ্যা অপর একটি সংখ্যার factor হলে, factor টি রেখে অপর সংখ্যা উপেক্ষা করা যায়।
Example: Find the L.C.M of 9,15,18,25
এক্ষেত্রে 9, 18 এর factor এবং 15 এর 3 ও 5, 183 25 এর factor, 183 25 এর L.C.M বের করলে উত্তর পাওয়া যাবে।

03. কিছু সংখ্যার H.C.F বের করার ক্ষেত্রে একটি সংখ্যা অপর একটি সংখ্যার factor হলে, factor টি রেখে অপর সংখ্যা উপেক্ষা করা যায়।
Example: Find the H.C.F of 9,18 and 21
এক্ষেত্রে 18 উপেক্ষা করে 9 ও 21 এবং H.C.F বের করলেই উত্তর পাওয়া যাবে।

04. যদি এমন কোন number নির্ণয় করতে বলা হয় যা কিছু number দিয়ে divisible তা হলে number গুলোর L.C.M বের করতে হবে।
Example: find the number which is divisible by 2, 3, 5 and 7
Ans. 210.

05. যদি সমান কোন number বের করতে বলা হয় যা কিছু সংখ্যা দিয়ে ভাগ করলে প্রত্যেক ক্ষেত্রে একই remainder থাকে তবে L.C.M এর সাথে remainder যোগ করতে হবে।
Example: আগের Ans. এর সাথে 1 যোগ করে দিলে প্রত্যেক ক্ষেত্রে 1 remainder থাকবে।

06. প্রদত্ত number গুলোর সম ব্যবধানের কিছু remainder অবশিষ্ট থাকলে L.C.M থেকে ব্যবধান বিয়োগ করতে হবে।
Example: 210 থেকে 1 বিয়োগ করলে অর্থাৎ 209 কে 2, 3, 5, 7 দিয়ে ভাগ করলে যথাক্রমে 1, 2, 4, ও 6 অবশিষ্ট থাকবে (এক্ষেত্রে ব্যবধান 1 )

7. কোন সংখ্যা যা দ্বারা কিছু সংখ্যা divisible বের করতে বললে H.C.F বের কতে হবে।

8. Fraction এর comparison বা addition বা Subtraction এর ক্ষেত্রে fraction গুলো একই denominator বিশিষ্ট (সমহর বিশিষ্ট) করতে হয়, সেক্ষেত্রে L.C.M ব্যবহার করে Least Common denominator (LCD) নির্ণয় করা হয়।

 

Prime numbers(মৌলিক সংখ্যা):

যে(সকল) (স্বাভাবিক)সংখ্যাকে 1 ও ঐ সংখ্যা ছাড়া অন্য কোন সংখ্যা দ্বারা নিঃশেষে ভাগ(divisible) করা যায় না, তাকে Prime numbers(মৌলিক সংখ্যা) বলে।

* মৌলিক সংখ্যার উৎপাদক(factor) দুইটি হয়- 1 ও ঐ সংখ্যাটি। যেমন- 5 এর মৌলিক সংখ্যা দুটি হচ্ছে: 1, 5 (= 5/1, 5/5) দ্বারা ভাগ করা যায়।

* 1 মৌলিক সংখ্যা নয়, কারণ এর উৎপাদক একটি (শুধু 1ই)।

* 2 হচ্ছে একমাত্র জোড়(even) prime nuumber.

 

# এ টপিকের Solving Teqniques Guidelines:

✔1-300 এর মধ্যে prime numbers গুলো মুখস্থ জানতে হবে। (ম্যাথগুল দ্রুত পারার জন্য)

✔কোন সংখ্যা Prime Number কিনা তা নির্ণয়ের সহজ পদ্ধতি টি জানতে হবে।

✔যেকোনো সংখ্যার square ভ্যালু (বর্গের নামটা) গুলা মুখস্থ জানতে হবে।

এক্ষেত্রে, দুই অঙ্কের যেকোনো সংখ্যার বর্গ নির্ণয়ের শর্টকাট নিয়মটি জানতে হবে।

এছাড়াও, দুইটি সংখ্যার গুনের শর্টকাট নিয়মটি জানতে হবে।

 

কোন সংখ্যা Prime Number কিনা তা নির্ণয়ের একটি সহজ পদ্ধতি:

➤ প্রথমে, number টির কাছাকাছি approximate root(বর্গমূল) সংখ্যাটি নির্ণয় করতে হবে।

➤ এরপর. numberটিকে ঐটার root number এর চেয়ে ছোট বা সমান prime numberগুলো দিয়ে ভাগ করতে হবে, এক্ষেত্রে-

– যদি,numberটি prime numberগুলোর যেকোনো একটি দিয়ে evenly divisible হয়, তবে numberটি Prime Number হবে না।

– আর,numberটি কোন ক্ষেত্রেই evenly divisible না হয়, তবে numberটি Prime Number.

Example: Is the number 191 prime?
➤ 191 এই number টির কাছাকাছি approximate root(বর্গমূল) সংখ্যাটি- 14, [14² = 196], 14² > 191

➤ 14 সংখ্যাটির চেয়ে ছোট Prime number গুলো হচ্ছে- 2, 3, 5, 7, 11, 13; তাই শুধু এগুলো দিয়েই টেস্টিং করলে হবে। এদের কোনটি দিয়েই 191 evenly divisible না। তাই 191 একটি prime number.

2 দিয়ে divisible কিনা তা চেক: যদি integer এর শেষ সংখ্যা(units digit)টি even or 0 হয়।
3 দিয়ে divisible কিনা তা চেক: যদি integer এর digit গুলোর sum 3 দিয়ে divisible(নিঃশেষে বিভাজ্য) হয়।
5 দিয়ে divisible কিনা তা চেক: যদি তার শেষ সংখ্যা(units digit)টি 0 বা 5 হয়।
7 দিয়ে divisible কিনা তা চেক: শেষ সংখ্যাতে ডবল(Double) করলে যা হয় সেটা মুল সংখ্যারর শেষ সংখ্যা ব্যাতিত বাকি সংখ্যা থেকে বিয়োগ(Subtract) দেব, এরপর ৭ দ্বারা ভাগ(divisible) করব। [বড় সংখ্যা হলে পর্যায়ক্রমে এভাবে করতে থাকব] যেমন- 191 এর last digit টির Double 1→2, বাকি সংখ্যা থেকে Subtract 19−2=17, যা 7 দ্বারা divisible নয়.
11 দিয়ে divisible কিনা তা চেক: যদি ডান দিক থেকে odd numbered place গুলোর sum of the digit এবং even numbered place গুলোর sum of the digit এর পার্থক্য 0 বা 11 দ্বারা divisible হয়।13 দিয়ে divisible কিনা তা চেক: শেষ সংখ্যাতে 4গুণ করলে যা হয় সেটা মুল সংখ্যারর শেষ সংখ্যা ব্যাতিত বাকি সংখ্যা থেকে বিয়োগ দেব, এরপর 13 দ্বারা ভাগ করব। (বড় সংখ্যা হলে পর্যায়ক্রমে এভাবে করতে থাকব।)

সাজেশনঃ 11,7,13 দিয়ে বিভাজ্য কিনা তা সবার আগে চেক করব। কারনসমুহ- 2,5 দিয়ে বিভাজ্য কিনা তা চোখের পলকে এমনি বুঝা যায়, আর ৩ দিয় দিয়ে বিভাজ্য কিনা তাও দ্রুত বের করা যায়।

শর্টকাট:

# দুই সংখ্যার গুণ করার নিয়ম (Allways কার্যকর)-

বিকল্প(সবচেয়ে সহজ নিয়ম): # দুই সংখ্যার গুণ করার নিয়ম / বর্গ করার নিয়ম(Allways কার্যকর)-
শর্টকাট গুণ করার নিয়ম

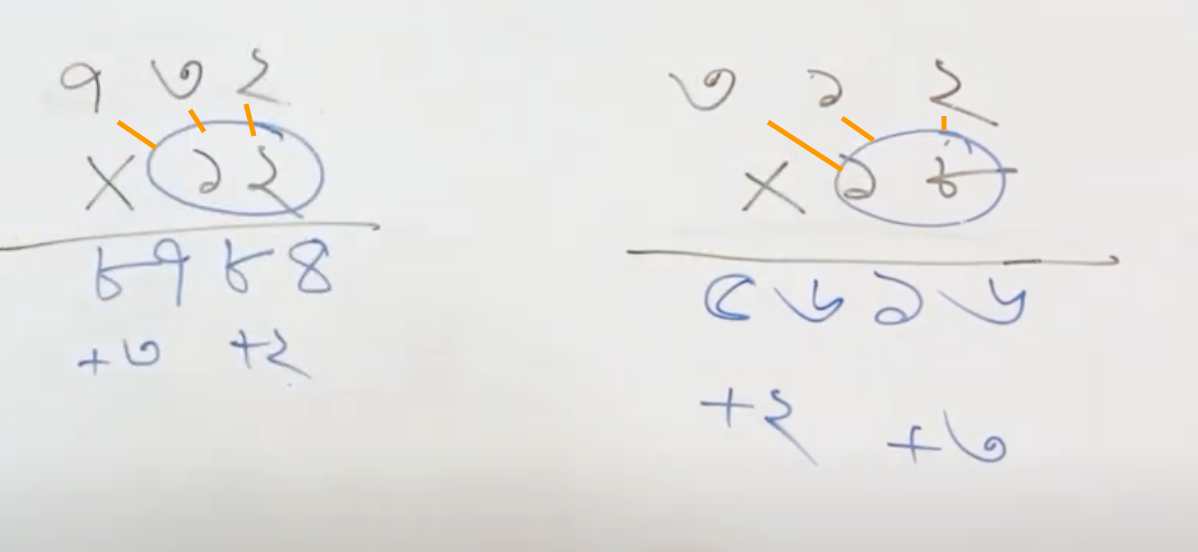
# ঘন করার নিয়ম- 

#

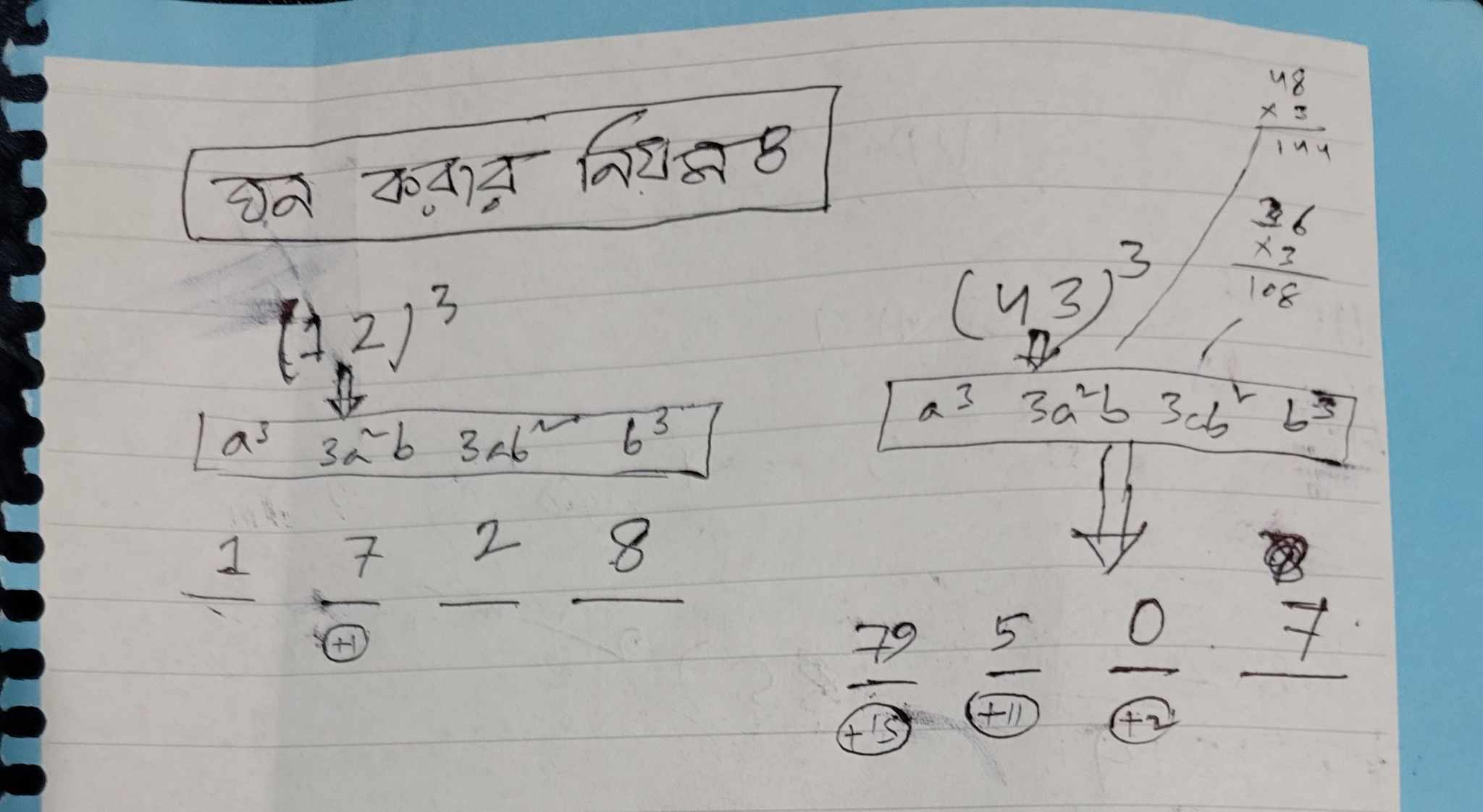
তিন সংখ্যার গুণ করার নিয়ম (Allways কার্যকর)-

অথবা,

 

 

1-100 এর মধ্যে prime numbers 25টি: (4422 3223 21 হচ্ছে শর্টকাট Memorize sequence টেকনিক)

• 2, 3, 5, 7,
• 11, 13, 17, 19,
• 23, 29,
• 31, 37,
• 41, 43, 47,
• 53, 59,
• 61, 67,71,
• 73, 79,
• 83, 89,
• 97

[Trap(prime nuumber নয়, কিন্তু তাও যেগুলোতে ভুল করতে পার): 53, 57, 63, 69, 77, 81, 87, 91, 93]

101-200 এর মধ্যে prime numbers 21টি: (4113 1222 14 হচ্ছে শর্টকাট Memorize sequence টেকনিক)

• 101,103,107,109
• 113
• 127
• 131,137, 139
• 149
• 151, 157
• 163, 167
• 173,179
• 181
• 191,193,197,199

[Trap(prime nuumber নয়, কিন্তু তাও যেগুলোতে ভুল করতে পার):[117, 123, 141, 143, 147, 153, 161, 171, 177, 183, 187]

201-300 এর মধ্যে prime numbers 15টি: (0132 1222 20 হচ্ছে শর্টকাট Memorize sequence টেকনিক)

• 211
• 223 227 229
• 233 239 –
• 241
• 251 257
• 263 269 –
• 271 277
• 281 283

(((

বর্গসংখ্যা:- কোনো স্বাভাবিক সংখ্যার বর্গ সংখ্যা হল ওই সংখ্যার গুণফল। যেমন- ২৫ = ৫ x ৫

বর্গমূলঃ কোন সংখ্যাকেও ঐ সংখ্যা দিয়ে গুণ করলে যে নতুন সংখ্যা পাওয়া যায় তার বর্গমূল হবে প্রথমোক্ত সংখ্যাটি। যেমন- 2^২ = 4

দশমিক সংখ্যার বর্গমূল-

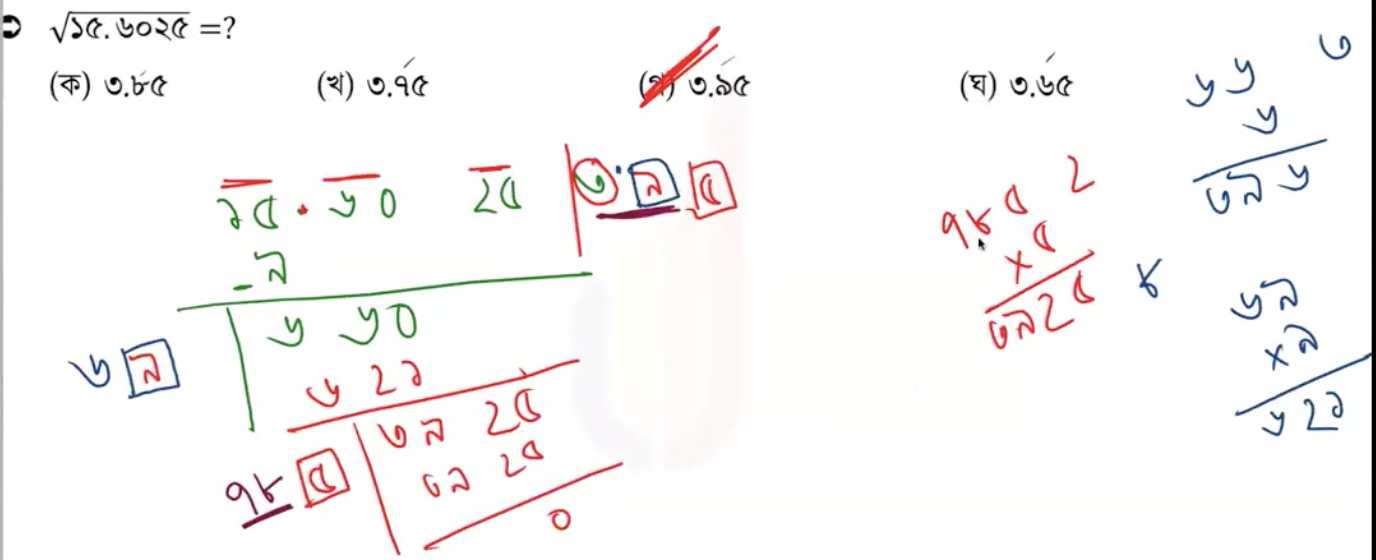
যে নামটা কাজে লাগবে:

(বর্গের নামটা)- [আপু বলছে square ভ্যালু গুলা মুখস্থ করে ফেলতে]

•  1² = 1
• 2² = 4
• 3² = 9
• 4² = 16
• 5² = 25
• 6² = 36
• 7² = 49
• 8² = 64
• 9² = 81
• 10² = 100
• 11² = 121
• 12² = 144
• 13² = 169
• 14² = 196
• 15² = 225
• 16² = 256
• 17² = 289
• 18² = 324
• 19² = 361
• 20² = 400
• 25² = 625

শর্টকাট করব-

• দুই অঙ্কের যেকোনো সংখ্যার বর্গ 
• তিন অঙ্কের যেকোনো সংখ্যার বর্গ

(ঘনের নামটা)-

•  1³ = 1
• 2³ = 8
• 3³ = 27
• 4³ = 64
• 5³ = 125
• 6³ = 216
• 7³ = 343
• 8³ = 512
• 9³ = 729
• 10³ = 1000

শর্টকাট করব-

• দুই অঙ্কের যেকোনো সংখ্যার ঘন 
• তিন অঙ্কের যেকোনো সংখ্যার ঘন

শর্টকাট – https://youtu.be/I1Ago5gSHeo

——————

১০-২০ এর নিচের দুটি সংখ্যার গুনঃ

——————

*** 2 এর পাওয়ারের নামটা শিখা:

•  2¹ = 2
• 2² = 4
• 2³ = 8
• 2⁴ = 16
• 2⁵ = 32
• 2⁶ = 64
• 2⁷ = 128
• 2⁸ = 256
• 2⁹ = 512
• 2¹⁰= 1024

*** 9 এর পাওয়ারের নামটা শিখা:

• 9¹ = 9
• 9² = 81
• 9³ = 729

*** 7 এর পাওয়ারের নামটা শিখা:

• 7¹ = 7
• 7² = 49
• 7³ = 343
• 7⁴ = 2401

*** 5 এর পাওয়ারের নামটা শিখা:

• 5¹ = 5
• 5² = 25
• 5³ = 125
• 5⁴ = 625
• 5⁵ = 3125

ও এর পূর্ণ বর্গ সংখ্যা 25 এর পাওয়ারের নামটা শিখা:

• ¹ =
• ² =
• ³ =
• ⁴ =
• ⁵ =
• ⁶ =
• ⁷ =

———–

Co-prime numbers(সহ-মৌলিক সংখ্যা):  দুইটি সংখ্যাকে Co-prime number বলা হব, যদি তাদের h.c.f 1 হয়। অর্থাৎ যখন ১ ছাড়া দুইটা সংখ্যার সাধারণ উৎপাদক থাকেনা, তখন তারা পরস্পর সহমৌলিক সংখ্যা। // Consider a set of two numbers, if they have no positive integer that can divide both, other than 1, the pair of numbers is co-prime.

Example: For 21 and 27:

• The factors of 21 are 1, 3, 7, 21.
• The factors of 27 are 1, 3, 9, 27.

Here 21 and 27 have two common factors; they are 1 and 3. HCF is 3 and they are not co-prime.

Co prime with	Co prime numbers pairs
1	(1, 2), (1, 3), (1, 4), (1, 5)  (1, 6),….., (1, 20),….
2	(2, 3), (2, 5), (2, 7), (2, 9), …, (2, 15),…..
3	(3, 4), (3, 5), (3, 7), (3, 10), (3, 11),…., (3, 20),…
4	(4, 5), (4, 7), (4, 9), (4, 11), (4, 13), (4, 15),….
5	(5, 6), (5, 7), (5, 8), (5, 9), (5, 11), (5, 12),…

Co-prime Numbers from 1 to 100: There are several pairs of co-primes from 1 to 100 which follow the above properties. Some of them are:

(13, 14)
(28, 57)
(1, 99)
(2, 97)
(46, 67)
(75, 41) and so on.

Composite numbe(অ-মৌলিক সংখ্যা/ যৌগিক সংখ্যা): 1 ও ঐ নাম্বার ছাড়াও এক/একাধিক number দিয়ে evenly divisible হলে সেটি Composite number. // একাধিক মৌলিক সংখ্যার গুণফল হিসেবে যেসকল সংখ্যাকে প্রকাশ করা যায়, সেগুলোই যৌগিক সংখ্যা। যেমন- 4.6,8,9,12, 10=5×2 etc.

 

Practice:

Q: Which of the following is a prime number?

         (a) 143                     (b) 289                     (c) 117                     (d) 359

Solution:

Clearly,

143 = 13 X 11 So, 143 is not prime.

289 = 17 X 17 So, 289 is not prime.

117 = 39 X 3   So, 117 is not prime.

359<(20)²; prime numbers less than 20 are 2, 3, 5. 7, 11, 13, 17, 19.

And, 359 is not exactly divisible by any of them.

So, 359 is a prime number.

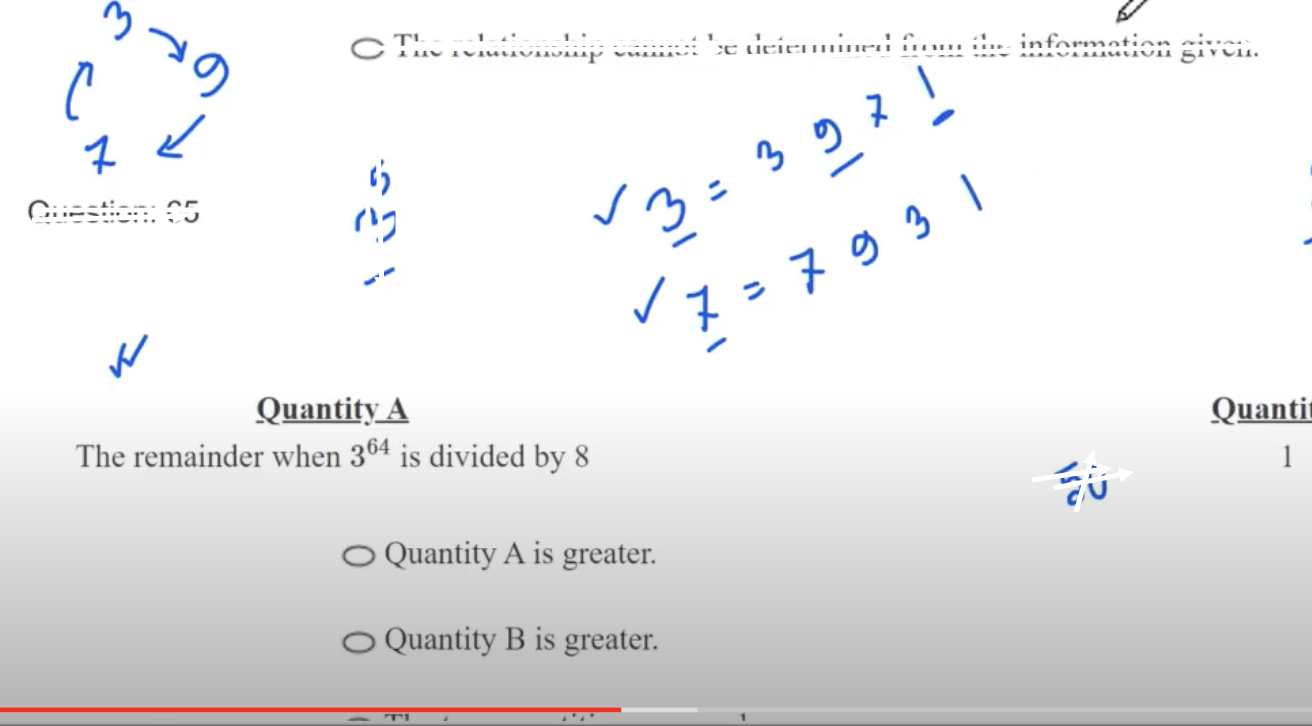
Q:

(A) Quantity A is greater.
(B) Quantity B is greater.
(C) The two quantities are equal.
(D) The relationship cannot be determined from the information given.

Solution:

the correct answer is: Choice A, Quantity A is greater.

Explanation: A>B

Quantity A is 29. Because, 29 is the least prime number greater than 24 (when the integers greater than 24 are 25, 26, 27, 28 are not prime numbers).

Quantity B is 23. Because, 29 is the greatest

Q: If a is the smallest prime number greater than 21 and b is the largest prime number less than 16, then ab =

A) 299

B) 323

C) 330

D) 345

E) 351

Solution:

Now, a is the smallest prime number greater than 21 (a = 23)
Similarly, b is the largest prime number lesser than 16 (b = 13)

Therefore, the value of ab = 23*13 = 299(ends with a 9 – Only option in answer options is Option A.

#

Main Topics: Fractions, Decimals, || Ratios-Proportion, || Percent

Extend Topics: Fractions, Decimals || Exponents, Square, Cube, Square root, Cube root || Real Number, Number Line, Absolute Value, Reciprocals || Ratios-Proportion || Percent

Inequalities and Absolute Value

negetive exponent ≠ Negetive Number

কয়েকটা মান মুখস্থ করতে হবে-

odd order root

even order root

 

[a < a3 < a4 < a2]

(-1 < a < 0)

 

#

Average, Ages

Numbers

Time & Distance

Work Problems

Set

Mixture Problems

#

সমান্তর ধারা সংক্রান্ত ১১ টি সূত্র এই একটি ভিডিওতে! Arithmetic Progression Related 11 Formulas!

 

Arithmetic Progression = সমান্তর ধারা,

Algebra

# Profit

# interest

Geometry

Basic terms

# ত্রিভুজের সংখ্যা নির্ণয়/গণনা:

 

#

 

 

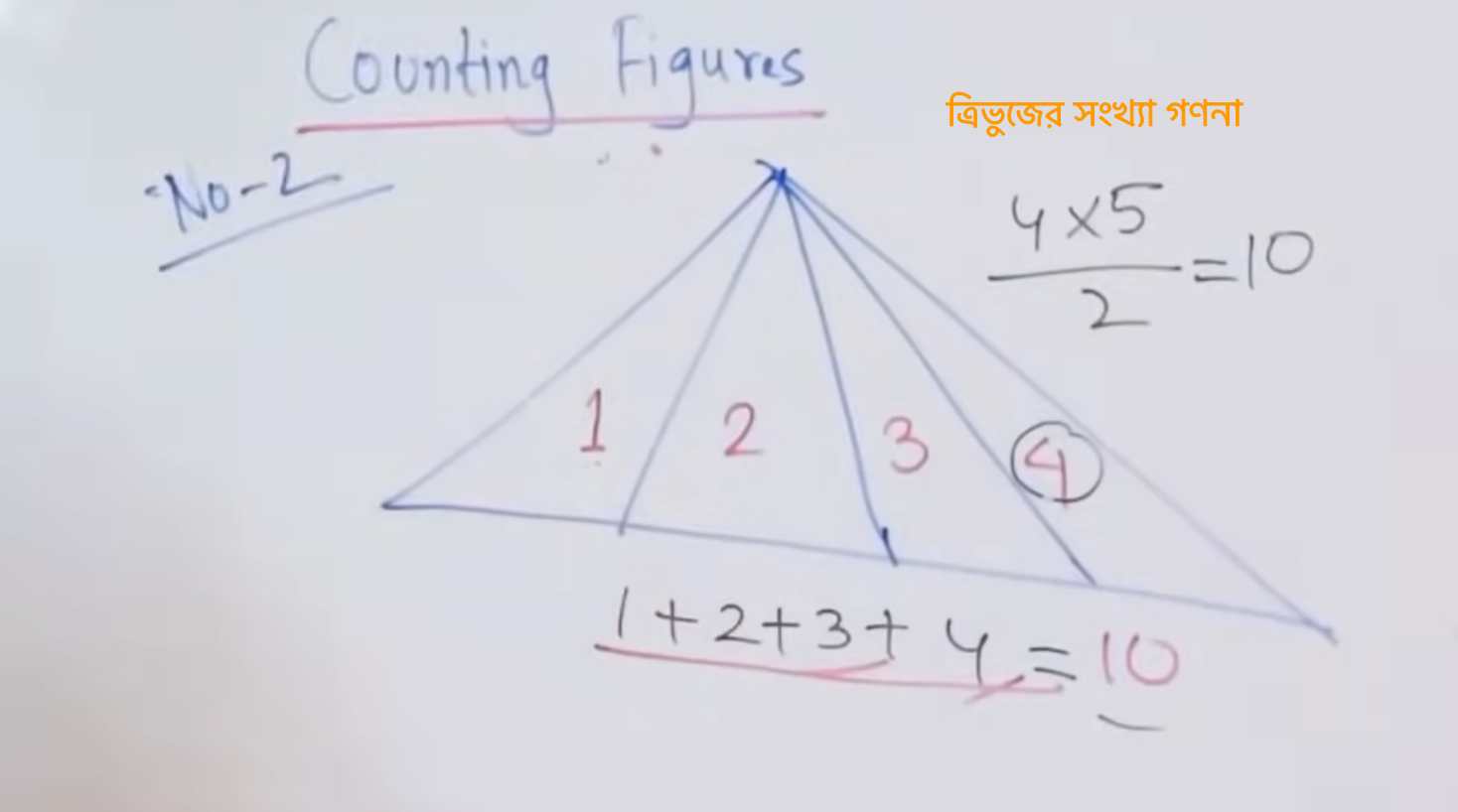
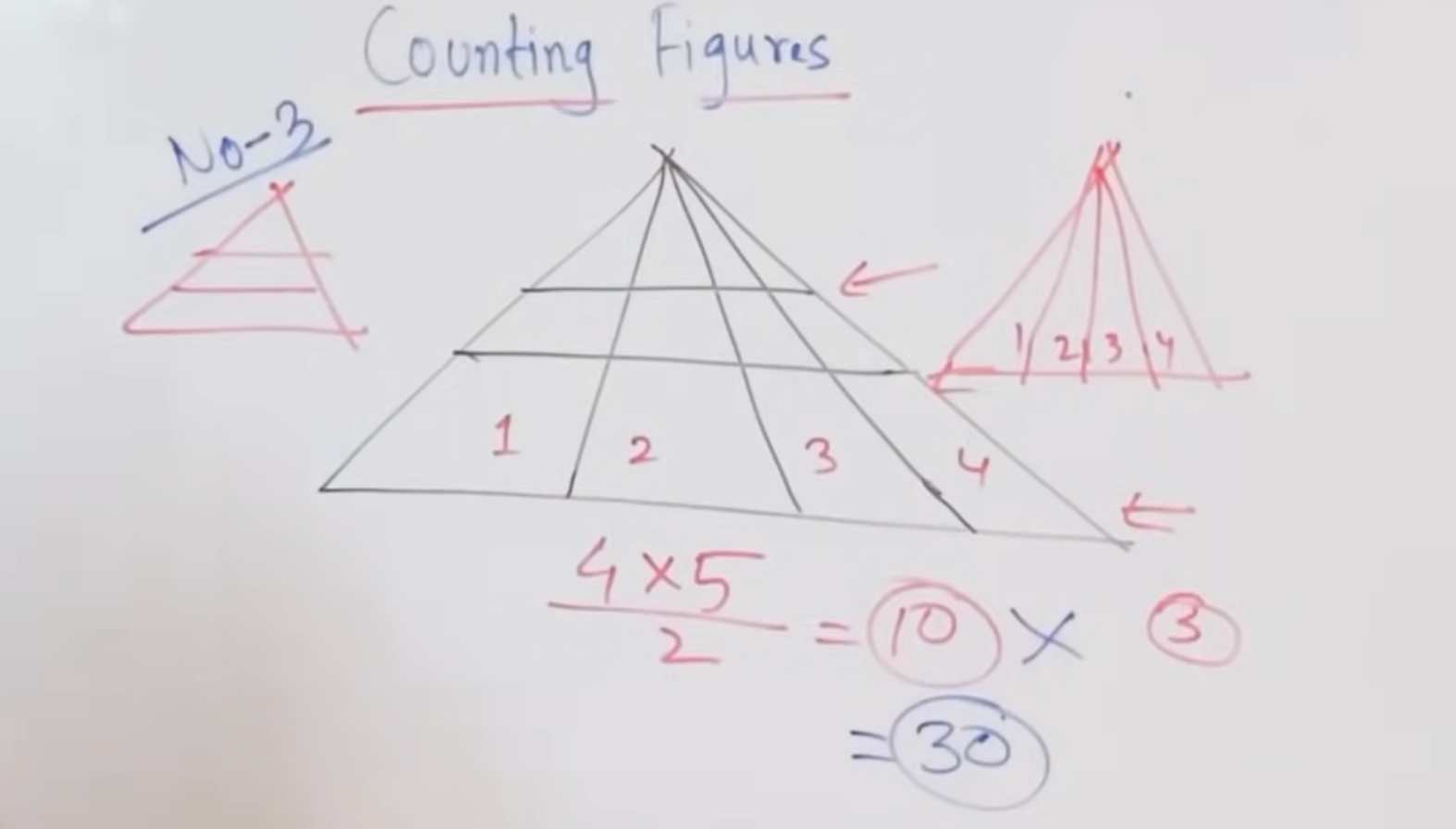
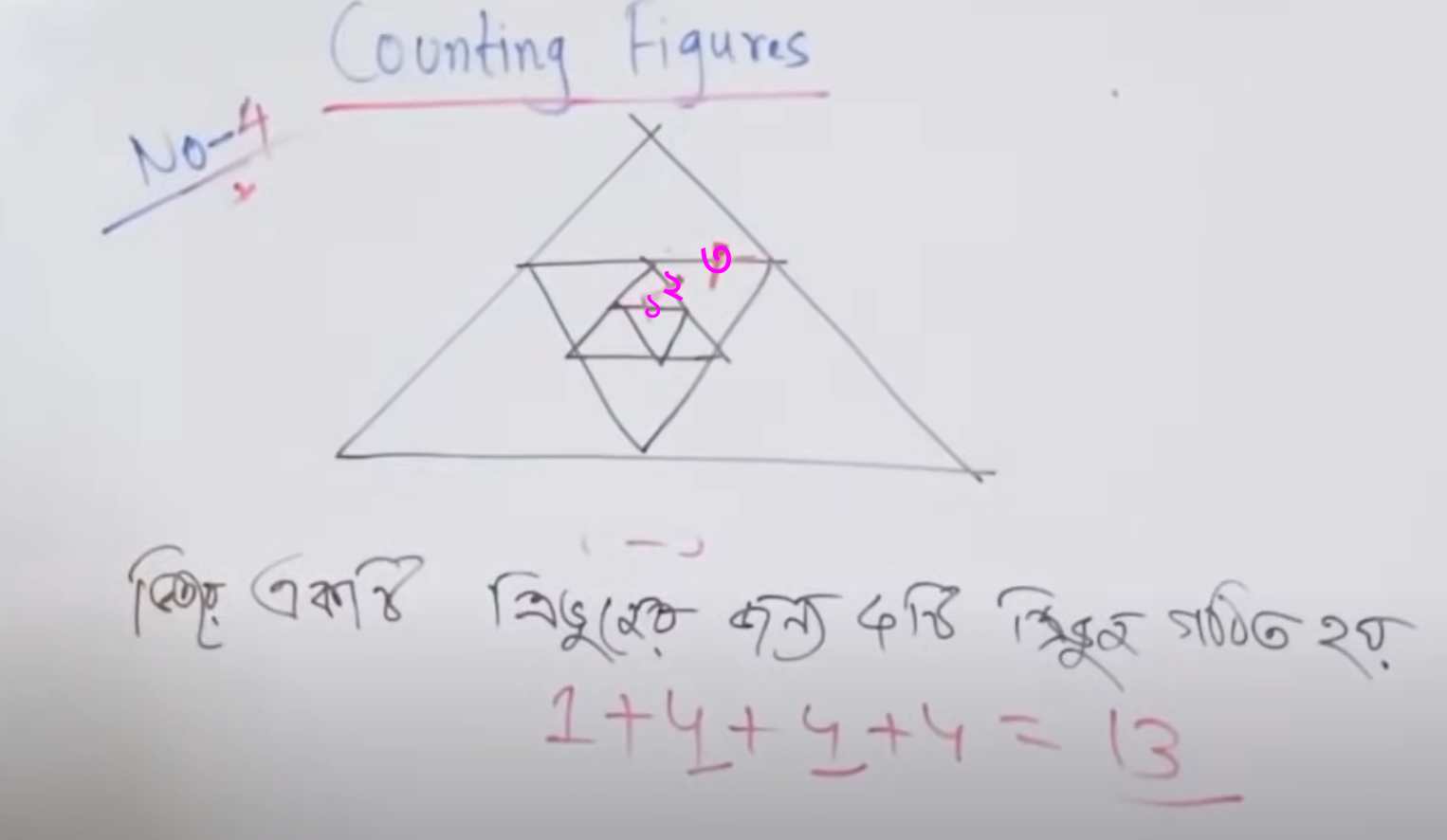
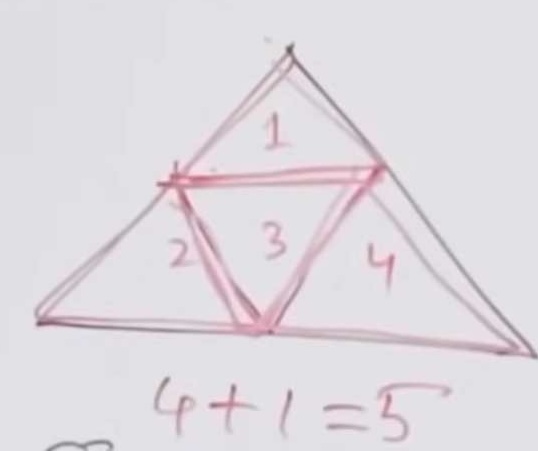
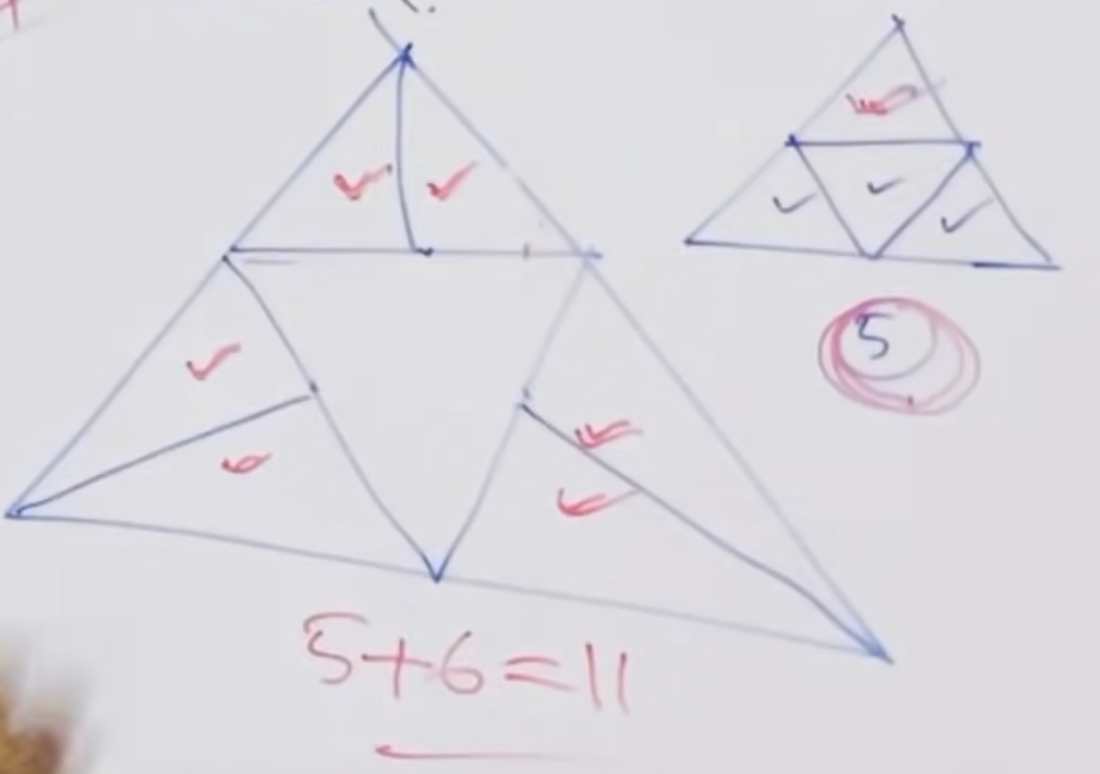
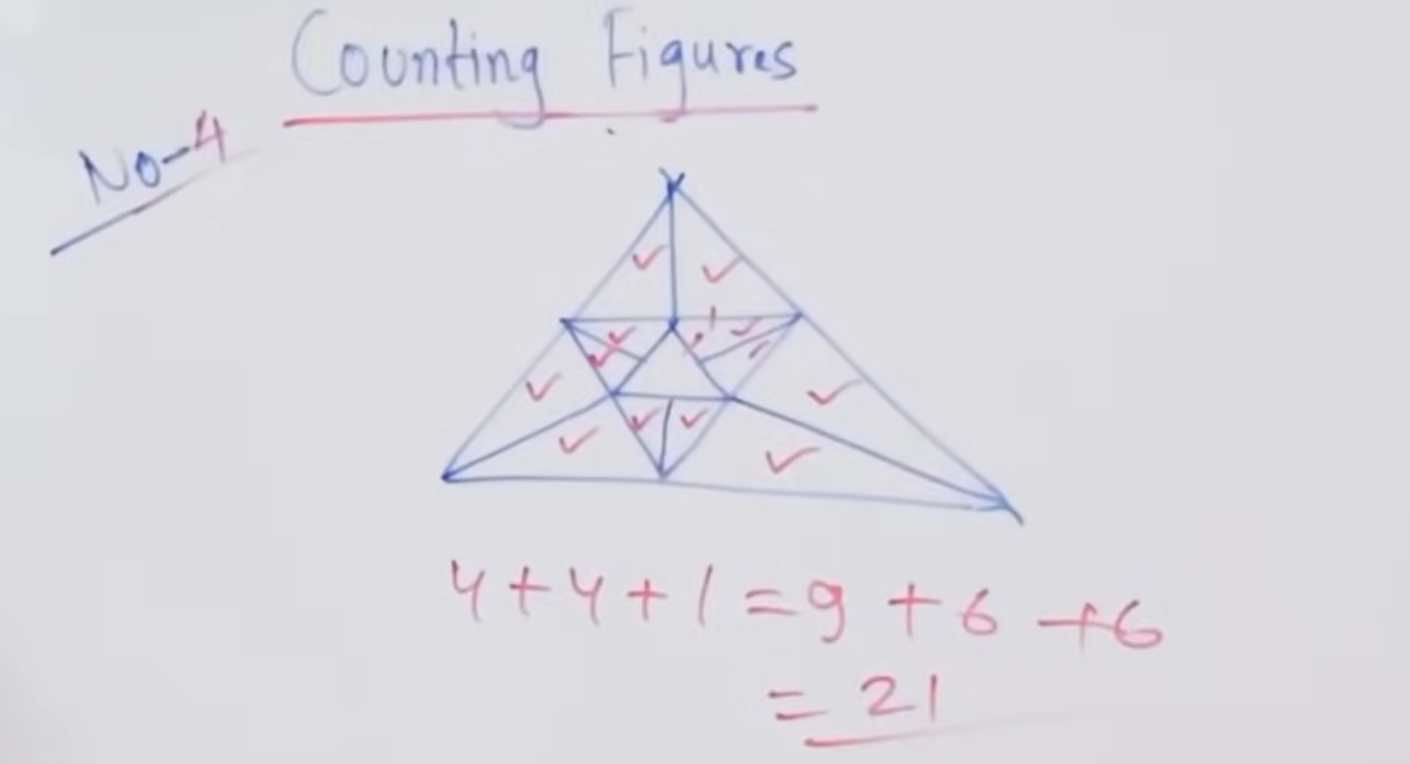
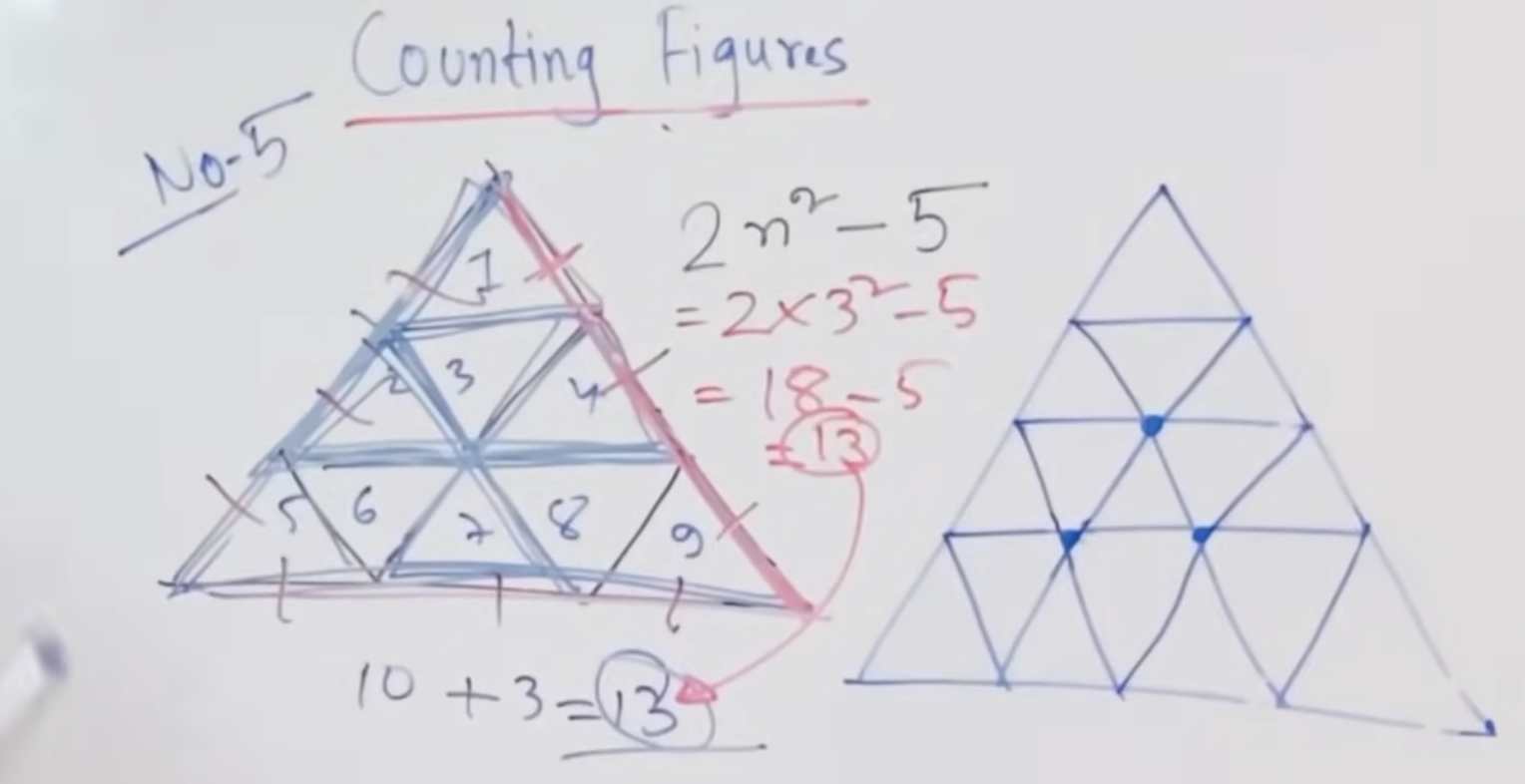
4. Data Analysis

Quartiles, Standard Deviation and Normal Distribution

আগে জেনেছি-

• sets
• Central tendency

আজকে জানব-

• Quantiles
• standard deviation
• Normal distribution(+ visualization)

Data Analysis এ আমাদের এক সেট ডেটা দেয়া থাকে। যেমন- {2,5,7,9,13, 27, 39}

আমরা জানি, Central tendency বলতে meaw(average) কিভাবে বের করতে হয় তা বুঝি।

ডেটা সেট এর প্রত্যেকটা elements যোগ করে ২ দিয়ে ভাগ করলেই আমরা meaw(average) ভ্যালুটা পেয়ে যাই। এক্ষেত্রে, কোনো নাম্বারের রিপিটেশন থাকলে সেটা mod হিসেবে কাজ করে।
Medium যখন বের করেছি তখনও meaw(average) ভ্যালু কোনটা সেটা বের করেছি।

Central tendency বের করার এই যে হিসাব নিকাশ same way টাই হল Quantiles.
Quantiles এর কাজ হল আমাদের যে ডেটাগুলো রয়েছে ডেটাগুলোকে সমানভাগে ভাগ করে ফেলা। যাতে আরও exact way তে সলিউশন বের করা যায়।
ধরি, আমাদের ডেটা ১৩টা{4, 8, 12, 15, 18, 21, 27, 39, 52, 63, 67, 77}, এগুলাকে সমান ৪ভাগে ভাগ করতে যেয়ে ৩বার ভাঙতে হয়(Q1,Q2,Q3)। এখানে, Q2 হচ্ছে total ডেটা(A) এর medium. [Q1 lower set(M).]

Meaw, mediaw, mode, Quantile

প্রশ্নঃ

১ম কাজ হবে, ডেটাগুলোকে সাজিয়ে নেয়া

Standard Deviation:

Standard Deviation || Powerful Formula || Masterpiece Discussion

 

Probability

Sub: topic in Probability:-

1. General Formula
2. Notation
3. Complement
4. OR rule
5. And rule
6. Mutually exclusive
7. Independent event
8. Conditional probability

 

Probability General Formula = no. of success(যে ফলাফলটা চাচ্ছি ঐ ফলাফল কয়টা আছে) / no. of outcome(total)

জেনে রাখুন,, # = number; অর্থাৎ হ্যাশট্যাগ দিয়ে নাম্বার কে বুঝায়।

উদা— লুডুতে ৬টা ভ্যালু থাকে- 1,2,3,4,5,6
ধরি, এক্ষেত্রে, 3 আসার সম্ভাবনা কত তা জানতে চাচ্ছি।
তাহলে, P(3) = 1/6
(কারণ 3 এখানে একটাই আছে, তাই 3 আসার সম্ভাবনা 1 বসানো হয়েছে)
ইংরেজি ভার্সনে করলে,
Event, A = 3
∴ P(A) = 1/6

Complement A = 1,2,4,5,6
∴ P(A’) = 5/6 = 1−1/6 = 1−P(A)
এখানে, Complement A এর মানে হচ্ছে A বাদে(বাদবাকি) সবকিছু।

# or – এর মানে (এটা অথবা ঐটা), + বোঝায়, দুইটা কন্ডিশন এর মধ্যে হয় এটা, না হয় ঐটা।(অর্থাৎ যেকোনো একটা হলেই হল)

P(3 or 6) = B = 3 or 6 হলে, [এখানে, Dice Roll ১ বার করা হচ্ছে]

∴ P(B) = 1/6 + 1/6 = 1/3 (এখানে, Probability বেশি)

# and – এর মানে (এটা ঐটা দুটাই), X বোঝায়।

P(3 and 6) = C = 3 and 6 হলে, [এখানে, Dice Roll 2 বার করা হচ্ছে]

∴ P(C) = 1/6 X 1/6 = 1/36 (এখানে, Probability কম)

যেমন-

• A AND B = 1 (এক্ষেত্রে, A=1, B=1)
• OR Gate সার্কিটে A OR B = 1 (A=1 হলে B=0,A=0 হলে B=1)

independent: এটা বুঝতে হলে আগে Mutual exclusive বুঝতে হবে।

Mutual exclusive: একটা হলে আরেকটা হবে (এক্ষেত্রে অবশ্যই ঘটনা দুইবার ঘটতে হবে)। না আর, Mutual exclusive হলেই or টা হবে, কিন্তু or দেখলেই Mutual exclusive বলা যাবে না।

যেমন- 1,2,3,4,5,6 (Roll 2 dice)

যদি A = 3, B = 6 হয় তাহলে P(A) ও P(B) হচ্ছে প্রত্যেকটা একেকটা independent.

independent:

conditional probability:

Parabola || Exceptional Formula 

All Daily Study Lessons List

kmf 11 videos by GREQuantSchool

Manhattan 5LB 48 videos

Facebook group question

Session’s Recording